题目内容
9.计算 $\sqrt{12}-{({\frac{1}{2}})^{-1}}+{({2-2\sqrt{5}})^0}$=2$\sqrt{3}$-1.分析 首先把$\sqrt{12}$化成2$\sqrt{3}$,然后根据负整数指数幂、零指数幂的运算方法,分别求出${(\frac{1}{2})}^{-1}$、${(2-2\sqrt{5})}^{0}$的值各是多少;最后根据实数的运算顺序,从左向右依次计算,求出算式的值是多少即可.
解答 解:$\sqrt{12}-{({\frac{1}{2}})^{-1}}+{({2-2\sqrt{5}})^0}$
=2$\sqrt{3}$-2+1
=2$\sqrt{3}$-1.
故答案为:2$\sqrt{3}$-1.
点评 (1)此题主要考查了实数的运算,要熟练掌握,解答此题的关键是要明确:在进行实数运算时,和有理数运算一样,要从高级到低级,即先算乘方、开方,再算乘除,最后算加减,有括号的要先算括号里面的,同级运算要按照从左到有的顺序进行.另外,有理数的运算律在实数范围内仍然适用.
(2)此题还考查了零指数幂的运算,要熟练掌握,解答此题的关键是要明确:①a0=1(a≠0);②00≠1.
(3)此题还考查了负整数指数幂的运算,要熟练掌握,解答此题的关键是要明确:①a-p=$\frac{1}{{a}^{p}}$(a≠0,p为正整数);②计算负整数指数幂时,一定要根据负整数指数幂的意义计算;③当底数是分数时,只要把分子、分母颠倒,负指数就可变为正指数.

练习册系列答案
相关题目
17.下列说法错误的是( )
| A. | 单项式x的系数和次数都是1 | |
| B. | $\frac{1}{2}$不是单项式 | |
| C. | 多项式3x2y+2xy-3x+y中一次项的系数分别是-3,1 | |
| D. | -$\frac{2xy}{3}$是系数为-$\frac{2}{3}$的二次单项式 |
18.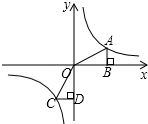 如图,A,C是函数$y=\frac{1}{x}$的图象上任意两点,过A作x轴的垂线,垂足为B,过C作y轴的垂线,垂足为D,记Rt△OAB的面积为S1,Rt△COD的面积S2,则( )
如图,A,C是函数$y=\frac{1}{x}$的图象上任意两点,过A作x轴的垂线,垂足为B,过C作y轴的垂线,垂足为D,记Rt△OAB的面积为S1,Rt△COD的面积S2,则( )
 如图,A,C是函数$y=\frac{1}{x}$的图象上任意两点,过A作x轴的垂线,垂足为B,过C作y轴的垂线,垂足为D,记Rt△OAB的面积为S1,Rt△COD的面积S2,则( )
如图,A,C是函数$y=\frac{1}{x}$的图象上任意两点,过A作x轴的垂线,垂足为B,过C作y轴的垂线,垂足为D,记Rt△OAB的面积为S1,Rt△COD的面积S2,则( )| A. | S1>S2 | B. | S1=S2 | C. | S1<S2 | D. | S1≥S2 |
19.三角形的两边长分别为4和5,第三边长是方程(x-4)(x-1)=0的解,则这个三角形的周长是( )
| A. | 10 | B. | 12 | C. | 13 | D. | 10或13 |
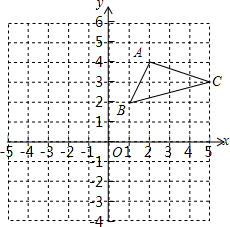 如图,在平面直角坐标系中,△ABC的三个顶点都在格点上,点A的坐标为(2,4).
如图,在平面直角坐标系中,△ABC的三个顶点都在格点上,点A的坐标为(2,4). 如图,已知∠EFD=∠BCA,BC=EF,AF=DC,则AB=DE.请通过完成以下填空的形式说明理由.
如图,已知∠EFD=∠BCA,BC=EF,AF=DC,则AB=DE.请通过完成以下填空的形式说明理由.