题目内容
2.已知关于x的一元二次方程x2+3x+m=0没有实数根,则m的取值范围是m>$\frac{9}{4}$.分析 先根据一元二次方程x2+3x+m=0得出a、b、c的值,再根据方程没有实数根列出关于m的不等式,求出m的取值范围即可.
解答 解:由一元二次方程x2+3x+m=0可知a=1,b=3,c=m,
∵方程没有实数根,
∴△=32-4m<0,
解得m>$\frac{9}{4}$.
故答案为m>$\frac{9}{4}$.
点评 本题考查的是一元二次方程根的判别式,根据题意列出关于m的不等式是解答此题的关键.

练习册系列答案
 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
15.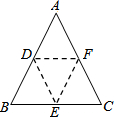 如图,D,E,F分别是等边△ABC的边AB,BC,CA的中点,现沿着虚线折起,使A,B,C三点重合,折起后得到的空间图形是( )
如图,D,E,F分别是等边△ABC的边AB,BC,CA的中点,现沿着虚线折起,使A,B,C三点重合,折起后得到的空间图形是( )
 如图,D,E,F分别是等边△ABC的边AB,BC,CA的中点,现沿着虚线折起,使A,B,C三点重合,折起后得到的空间图形是( )
如图,D,E,F分别是等边△ABC的边AB,BC,CA的中点,现沿着虚线折起,使A,B,C三点重合,折起后得到的空间图形是( )| A. | 棱锥 | B. | 圆锥 | C. | 棱柱 | D. | 正方体 |
 观察日历:
观察日历: