题目内容
13．若ax2+2x+$\frac{a}{8}$=（2x+$\frac{1}{2}$）2+m，则a=4，m=$\frac{1}{4}$．分析 已知等式右边利用完全平方公式化简，即可确定出a与m的值．
解答 解：∵ax2+2x+$\frac{a}{8}$=（2x+$\frac{1}{2}$）2+m=4x2+2x+$\frac{1}{4}$+m，
∴a=4，m=$\frac{1}{4}$，
故答案为：4；$\frac{1}{4}$
点评 此题考查了配方法的应用，熟练掌握完全平方公式是解本题的关键．
练习册系列答案
相关题目
1．要得到二次函数y=x2+4x-2的图象，需将y=x2的图象（ ）
| A． | 向左平移2个单位，再向下平移6个单位 | |
| B． | 向右平移2个单位，再向上平移2个单位 | |
| C． | 向左平移4个单位，再向上平移6个单位 | |
| D． | 向右平移4个单位，再向下平移1个单位 |
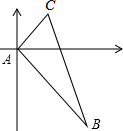如图，甲、乙两船从港口A同时出发，甲船以10海里/时速度向北偏东40°航行，乙船向南偏东50°航行，2.5小时后，甲船到达C岛，乙船到达B岛．若C、B两岛相距65海里，问乙船的航速是多少？
3．下列计算中，错误的是（ ）
| A． | （-2）+（+2）=0 | B． | （-6）+（+4）=-10 | C． | 0+（-3）=-3 | D． | （+$\frac{5}{6}$）+（-$\frac{1}{6}$）=$\frac{2}{3}$ |