题目内容
如图1—106所示，AD 为ABC的角平分线，DE⊥AC于点E，DF⊥AB于点F，
EF交AD于点M，求证AM⊥EF．
证明：因为AD平分∠BAC，DE⊥AC，DF⊥AB，所以DF=DE．
 |  |
在Rt△ADF和Rt△ADE中，
所以Rt△ADF≌Rt△AD（HL）．所AF=AE．在△AMF和△AME中，
所以△AMF≌△AME（ＳＡＳ），所以∠AMF=∠AME．又因为∠AMF＋∠AME=180°，所以∠AMF=∠AME=90°，即AM⊥EF
练习册系列答案
相关题目
∶1∶2 B．1∶2∶
D．2∶1∶
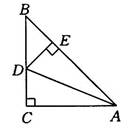
）如图1-110（3）所示，在AABC中，如果∠ACB不是直角，而（1）中的其他条件不变，那么（1）中所得的结论是否仍然成立？若成立，请证明；若不成立，请说明理由．
．
2×1×
；
2×(－2)×5；⑸
．
的解集为x＞1，那么a的取值范围是（ ）