题目内容
7.有6张正面分别标有数字-2,-1,0,2,4,6的不透明卡片,它们除数字不同外其余全部相同,现将它们背面朝上,洗匀后从中任取一张,将该卡片上的数字记为a,则使关于x的不等式$\left\{\begin{array}{l}{2x>3x-3}\\{3x-a>5}\end{array}\right.$有实数解的概率为$\frac{2}{3}$.分析 首先求得关于x的不等式$\left\{\begin{array}{l}{2x>3x-3}\\{3x-a>5}\end{array}\right.$有实数解时,a的取值范围,再利用概率公式即可求得答案.
解答 解:$\left\{\begin{array}{l}{2x>3x-3①}\\{3x-a>5②}\end{array}\right.$,
由①得:x<3,
由②得:x>$\frac{a+5}{3}$,
∴当$\frac{a+5}{3}$<3,即a<4时,关于x的不等式$\left\{\begin{array}{l}{2x>3x-3}\\{3x-a>5}\end{array}\right.$有实数解,
∴使关于x的不等式$\left\{\begin{array}{l}{2x>3x-3}\\{3x-a>5}\end{array}\right.$有实数解的概率为:$\frac{4}{6}$=$\frac{2}{3}$.
故答案为:$\frac{2}{3}$.
点评 此题考查了概率公式的应用.用到的知识点为:概率=所求情况数与总情况数之比.

练习册系列答案
 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案 名题金卷系列答案
名题金卷系列答案
相关题目
3.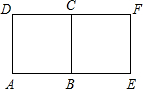 如图,由正方形ABCD通过一次旋转得到正方形BCFE,其可能的旋转中心有( )个.
如图,由正方形ABCD通过一次旋转得到正方形BCFE,其可能的旋转中心有( )个.
 如图,由正方形ABCD通过一次旋转得到正方形BCFE,其可能的旋转中心有( )个.
如图,由正方形ABCD通过一次旋转得到正方形BCFE,其可能的旋转中心有( )个.| A. | 1 | B. | 2 | C. | 3 | D. | 4 |