题目内容
16.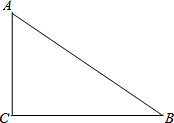 如图,已知△ABC,∠C=90°,AC<BC,若D为BC上一点,且到A,B两点距离相等.
如图,已知△ABC,∠C=90°,AC<BC,若D为BC上一点,且到A,B两点距离相等.(1)利用尺规,作出点D的位置(不写作法,保留作图痕迹);
(2)连结AD,若AB=5,AC=3,求CD的长.
分析 (1)作AB的垂直平分线交BC于D点,则DA=DB;
(2)先Rt△ABC中利用勾股定理计算出BC=4,设CD的长为x,则BD的长为(4-x),所有AD=BD=4-x,然后在Rt△ACD中利用勾股定理得到32+x2=(4-x)2,再解方程求出x即可.
解答 解:(1)如图,点D为所作;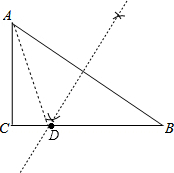
(2)在Rt△ABC中,BC=$\sqrt{A{B}^{2}-A{C}^{2}}$=$\sqrt{{5}^{2}-{3}^{2}}$=4,
设CD的长为x,则BD的长为(4-x),
由题意得AD=BD=4-x,
在Rt△ACD中,∵AC2+CD2=AD2,
∴32+x2=(4-x)2,
解得$x=\frac{7}{8}$,
∴CD的长为$\frac{7}{8}$.
点评 本题考查了作图-复杂作图:复杂作图是在五种基本作图的基础上进行作图,一般是结合了几何图形的性质和基本作图方法.解决此类题目的关键是熟悉基本几何图形的性质,结合几何图形的基本性质把复杂作图拆解成基本作图,逐步操作.也考查了勾股定理.

练习册系列答案
相关题目
6.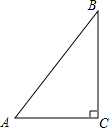 如图,在Rt△ABC中,∠C=90°,AC=3,BC=4,则cosA的值为( )
如图,在Rt△ABC中,∠C=90°,AC=3,BC=4,则cosA的值为( )
 如图,在Rt△ABC中,∠C=90°,AC=3,BC=4,则cosA的值为( )
如图,在Rt△ABC中,∠C=90°,AC=3,BC=4,则cosA的值为( )| A. | $\frac{3}{5}$ | B. | $\frac{5}{3}$ | C. | $\frac{4}{5}$ | D. | $\frac{3}{4}$ |
11. 如图,在△ABC中,D为BC上一点,且AB=AD=DC,∠B=80°,则∠C等于( )
如图,在△ABC中,D为BC上一点,且AB=AD=DC,∠B=80°,则∠C等于( )
 如图,在△ABC中,D为BC上一点,且AB=AD=DC,∠B=80°,则∠C等于( )
如图,在△ABC中,D为BC上一点,且AB=AD=DC,∠B=80°,则∠C等于( )| A. | 20° | B. | 30° | C. | 40° | D. | 50° |
5.下列语句中,正确的是( )
| A. | -$\frac{1}{3}$x=5的解是x=-$\frac{3}{5}$ | B. | 7x=-4的解是x=-$\frac{7}{4}$ | ||
| C. | -x=0的解是x=-1 | D. | $\frac{x}{-10}=0$的解是x=0 |
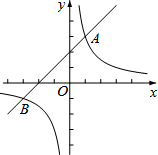 如图,一次函数y=x+2的图象与反比例函数y=$\frac{k}{x}$(k≠0)的图象交于A,B两点,且点A的坐标为(1,m).
如图,一次函数y=x+2的图象与反比例函数y=$\frac{k}{x}$(k≠0)的图象交于A,B两点,且点A的坐标为(1,m). 已知:如图,AB是⊙O的直径,AB=6,点C,D在⊙O上,且CD平分∠ACB,∠CAB=60°.
已知:如图,AB是⊙O的直径,AB=6,点C,D在⊙O上,且CD平分∠ACB,∠CAB=60°.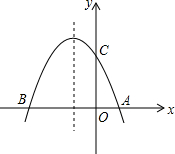 如图,抛物线y=ax2+bx+c与x轴交于A、B两点,与y轴交于C点,且A(1,0),C(0,3),抛物线的对称轴为x=-1.
如图,抛物线y=ax2+bx+c与x轴交于A、B两点,与y轴交于C点,且A(1,0),C(0,3),抛物线的对称轴为x=-1.