题目内容
 如图,已知抛物线y=-x2+4x(x≥0)与抛物线y=
如图,已知抛物线y=-x2+4x(x≥0)与抛物线y=| 1 |
| 3 |
(1)求点A的坐标;
(2)求出四边形OCAB的面积S与t的函数关系式,当S有最大值时t的值是多少?
(3)当直线运动到何位置即t为何值时,四边形OCAB为梯形?
考点:二次函数综合题
专题:
分析:(1)解抛物线的解析式组成的方程组的解即可求得.
(2)根据S四边形ABOC=S△OBC+S△ABC即可求得.
(3)有两种情况①AB∥OC,②OB∥AC,分别求得它们的解析式,如果两直线平行,则直线的斜率相等,即可求得t的值.
(2)根据S四边形ABOC=S△OBC+S△ABC即可求得.
(3)有两种情况①AB∥OC,②OB∥AC,分别求得它们的解析式,如果两直线平行,则直线的斜率相等,即可求得t的值.
解答:解:(1)解
得
或
,
∴A点的坐标为(3,3);

(2)如图所示:作AE∥y轴,直线x=t与抛物线y=-x2+4x的交点B(t,-t2+4t),与抛物线y=
x2的交点C(t,
t2);
∵A(3,3),
∴S四边形ABOC=S△OBC+S△ABC=
BC•OD+
BC•DE=
(-t2-4t-
t2)×t+
(-t2-4t-
t2)×(3-t)
整理得;S四边形ABOC=-2t2+6t=-2(t-
)2+
;
∴当t=
时,S四边形ABOC有最大值=
;
(3)有两种情况,
①当AB∥OC时,∵A(3,3),B(t,-t2+4t),C(t,
t2);
∴直线AB的解析式为:y=(1-t)x+3t,直线OC的解析式为:y=
tx2,
∴1-t=
t,
解得t=
;
②当OB∥AC时,
∵A(3,3),B(t,-t2+4t),C(t,
t2);
∴直线OB的解析式为:y=(-t+4)x,
直线AC的解析式为:y=
(t+3)x-t,
∴-t+4=
(t+3),
解得t=
;
∴当t=
或t=
时,四边形OCAB为梯形.
|
|
|
∴A点的坐标为(3,3);

(2)如图所示:作AE∥y轴,直线x=t与抛物线y=-x2+4x的交点B(t,-t2+4t),与抛物线y=
| 1 |
| 3 |
| 1 |
| 3 |
∵A(3,3),
∴S四边形ABOC=S△OBC+S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
整理得;S四边形ABOC=-2t2+6t=-2(t-
| 3 |
| 2 |
| 9 |
| 2 |
∴当t=
| 3 |
| 2 |
| 9 |
| 2 |
(3)有两种情况,
①当AB∥OC时,∵A(3,3),B(t,-t2+4t),C(t,
| 1 |
| 3 |
∴直线AB的解析式为:y=(1-t)x+3t,直线OC的解析式为:y=
| 1 |
| 3 |
∴1-t=
| 1 |
| 3 |
解得t=
| 3 |
| 4 |
②当OB∥AC时,
∵A(3,3),B(t,-t2+4t),C(t,
| 1 |
| 3 |
∴直线OB的解析式为:y=(-t+4)x,
直线AC的解析式为:y=
| 1 |
| 3 |
∴-t+4=
| 1 |
| 3 |
解得t=
| 9 |
| 4 |
∴当t=
| 3 |
| 4 |
| 9 |
| 4 |
点评:本题考查了两个抛物线的交点的求法,四边形面积的求法,以及梯形的判定方法,构建三角形是求四边形面积的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
下列调查中,适合采用全面调查(普查)方式的是( )
| A、对长江水质情况的调查 |
| B、对端午节期间市场上粽子质量情况的调查 |
| C、对某班40名同学体重情况的调查 |
| D、对某类烟花爆竹燃放安全情况的调查 |
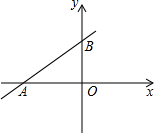 如图,已知直线l:y=
如图,已知直线l:y= 甲、乙两人从顺义少年宫出发,沿相同的线路跑向顺义公园,甲先跑一段路程后,乙开始出发,当乙超过甲150米时,乙停在此地等候甲,两人相遇后,乙和甲一起以甲原来的速度跑向顺义公园,如图是甲、乙两人在跑步的全过程中经过的路程y(米)与甲出发的时间x(秒)的函数图象,请根据题意解答下列问题.
甲、乙两人从顺义少年宫出发,沿相同的线路跑向顺义公园,甲先跑一段路程后,乙开始出发,当乙超过甲150米时,乙停在此地等候甲,两人相遇后,乙和甲一起以甲原来的速度跑向顺义公园,如图是甲、乙两人在跑步的全过程中经过的路程y(米)与甲出发的时间x(秒)的函数图象,请根据题意解答下列问题.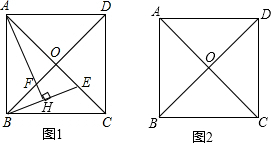 如图,已知正方形ABCD,AC、BD相交于点O,E为AC上一点,AH⊥EB交EB于点H,AH交BD于点F.
如图,已知正方形ABCD,AC、BD相交于点O,E为AC上一点,AH⊥EB交EB于点H,AH交BD于点F.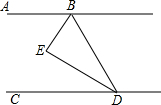 如图,已知,BE平分∠ABD,DE平分∠BDC,且∠EBD+∠EDB=90°.
如图,已知,BE平分∠ABD,DE平分∠BDC,且∠EBD+∠EDB=90°.