Question

【题目】综合与实践

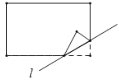
动手实践：数学课上老师让学生们折矩形纸片下面几幅图是学生们折出的一部分图形（沿直线折叠）由于折痕所在的直线不同，折出的图形也不同，各个图形中所“隐含的”基本图形也不同．我们可以通过发现基本图形研究这些图形中几何问题．

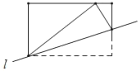
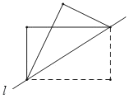
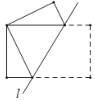
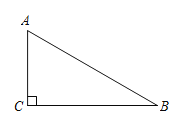
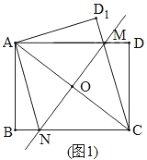
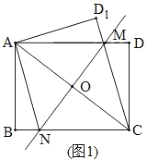
问题解决：（1）如图1，将矩形纸片沿直线折叠，使得点与点重合，点落在点的位置，连接，，，线段交于点，则与的关系为 ，线段与线段的关系为 ．

小强量得，则 ．

小丽说：“四边形是菱形”，请你帮她证明．

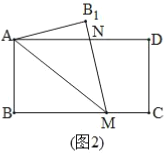
拓展延伸：（2）如图2，矩形纸片中，，，小明将矩形纸片沿直线折叠，点落在点的位置，交于点，请你直接写出线段的长： ．

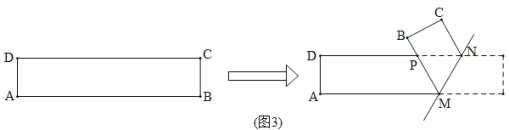
综合探究：（3）如图3，是一张矩形纸片，，．在矩形的边上取一点，在上取一点，将纸片沿折叠，使线段与线段交于点，得到．请你确定面积的取值范围 ．

Answer 1

【答案】（1）全等，垂直，80°，证明见解析；（2）；（3）

【解析】

（1）矩形纸片沿直线折叠，点落在点的位置，得，因为，所以≌，证明≌，可得MN⊥AC；已知，所以，可得，根据AD∥BC，得出，所以；

证明△ANO≌△AMO，根据对角线互相垂直平分的四边形是菱形来判定四边形是菱形．

（2）过点M作ME⊥AD，交AD于E，设NE=x，MN=，B1N=4-，AN=4-x，

在Rt△AB1M中利用勾股定理可求出x，即可求出ND

（3）先求△MNP面积的最小值，过点M作ME⊥DN，垂足为E，已知ME=AD=1，∠PNM=∠PMN，可得MP=NP，根据MPME，可得NP1，所以△MNP的面积值大于等于；

然后求△MNP面积可以取到的最大值，分两种情况讨论，情况一：将矩形纸片对折，使点B与D重合，此时点P也与D重合．情况二：将矩形纸片沿对角线AC对折，此时折痕即为AC，分别求解△MNP的面积，此时为△MNP面积可取到的最大值，综上所示即可求解出△MNP面积的取值范围．

（1）∵矩形纸片沿直线折叠，点落在点的位置

∴

又∵

∴≌

∵矩形纸片沿直线折叠，点落在点的位置

∴≌

∴∠AOM=∠COM=90°

∴MN⊥AC

∵

∴

∵NA=NC

∴

∵AD∥BC

∴

∴

∵MN⊥AC

∴

∵，AO=AO

∴△ANO≌△AMO

∴ON=OM

又∵OA=OC，MN⊥AC

∴四边形是菱形

故答案为：全等，垂直，80°，证明见解析

（2）过点M作ME⊥AD，交AD于E

设NE=x

MN=，B1N=4-，AN=4-x

在Rt△AB1M中

(4-x)2=32+(4-)2

解得x=

∴ND=NE+ED=2+=

故答案为：

（3）过点M作ME⊥DN，垂足为E，

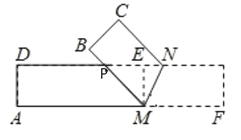
ME=AD=1．

∵∠PNM=∠PMN，

∴MP=NP，

又∵MPME，

∴NP1．

∴△MNP的面积=NPME

∴△MNP的面积大于等于

情况一：将矩形纸片对折，使点B与D重合，此时点P也与D重合．

MP=MB=x，则AM=5x

由勾股定理得12+（5-x）2=x2

解得x=2.6

∴MD=ND=2.6

S△MNP==1.3

情况二：将矩形纸片沿对角线AC对折，此时折痕即为AC

MP=AP=CP=x，则DP=5x

同理可得：MP=NP=2.6

∵MD=1，

∴S△MNP==1.3

△MNP的面积最大值为1.3．

综上所述面积的取值范围为≤S△MNP≤1.3