题目内容
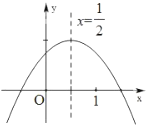
【题目】如图,二次函数![]() 的图象与
的图象与![]() 轴正半轴相交,其顶点坐标为
轴正半轴相交,其顶点坐标为![]() ,下列结论:①
,下列结论:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() .其中正确的个数是( ).
.其中正确的个数是( ).
A.1B.2C.3D.4
【答案】C
【解析】
由抛物线开口方向得到a<0,由抛物线与y轴的交点在x轴上方得到c>0,可对①进行判断;由抛物线的对称轴为直线x=![]() ,得到a+b=0,可对②进行判断;当x=-1时,由图象可知y<0,即可对③进行判断;根据顶点坐标为
,得到a+b=0,可对②进行判断;当x=-1时,由图象可知y<0,即可对③进行判断;根据顶点坐标为![]() ,代入函数解析式,以及抛物线的对称轴为
,代入函数解析式,以及抛物线的对称轴为![]() ,可对④进行判断.
,可对④进行判断.
①∵由图象可知抛物线开口向下
∴a<0
∵抛物线与y轴的交点在x轴上方
∴c>0
∴![]()
故①正确
②∵抛物线的对称轴为直线x=![]()
∴![]()
∴![]()
故②正确
③当x=-1时,由图象可知y<0
∴y=a-b+c<0
∴a+c<b
故③错误
④∵抛物线顶点坐标为![]()
∴![]()
∵b=-a
∴![]()
∴![]()
故④正确
综上所述①②④正确
故选:C

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
【题目】若一个函数当自变量在不同范围内取值时,函数表达式不同,我们称这样的函数为分段函数.下面我们参照学习函数的过程与方法,探究分段函数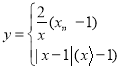 的图象与性质.列表:
的图象与性质.列表:
x | … |
|
|
|
|
|
| 0 |
| 1 |
| 2 |
| 3 | … |
y | … |
|
| 1 |
| 2 |
| 1 |
| 0 |
| 1 |
| 2 | … |
描点:在平面直角坐标系中,以自变量x的取值为横坐标,以相应的函数值y为纵坐标,描出相应的点,如图所示.
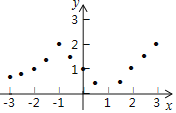
(1)如图,在平面直角坐标系中,观察描出的这些点的分布,作出函数图象;
(2)研究函数并结合图象与表格,回答下列问题:
①点![]() ,
,![]() ,
,![]() ,
,![]() 在函数图象上,
在函数图象上,![]()
![]() ,
,![]()
![]() ;(填“>”,“=”或“<”)
;(填“>”,“=”或“<”)
②当函数值![]() 时,求自变量x的值;
时,求自变量x的值;
③在直线![]() 的右侧的函数图象上有两个不同的点
的右侧的函数图象上有两个不同的点![]() ,
,![]() ,且
,且![]() ,求
,求![]() 的值;
的值;
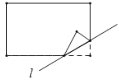
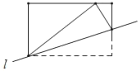
④若直线![]() 与函数图象有三个不同的交点,求a的取值范围.
与函数图象有三个不同的交点,求a的取值范围.