题目内容
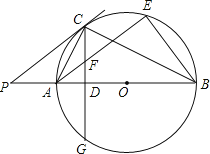
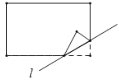
【题目】如图,抛物线![]() 与
与![]() 轴交于
轴交于![]() 两点,直线
两点,直线![]() 经过点
经过点![]() ,与抛物线的另一个交点为点
,与抛物线的另一个交点为点![]() ,点
,点![]() 的横坐标为3,线段
的横坐标为3,线段![]() 在线段
在线段![]() 上移动,
上移动,![]() =1,分别过点
=1,分别过点![]() 作
作![]() 轴的垂线,交抛物线于
轴的垂线,交抛物线于![]() ,交直线于
,交直线于![]() .
.
(1)求抛物线的解析式;
(2)当四边形DEFG为平行四边形时,求出此时点P,Q的坐标;
(3)在线段PQ的移动过程中,以D,E,F,G为顶点的四边形面积是否有最大值,若有求出最大值,若没有请说明理由.

【答案】(1)y=-![]() x2+
x2+![]() x+2;(2)P(
x+2;(2)P(![]() ,0),Q(
,0),Q(![]() ,0);(3)x=
,0);(3)x=![]() 时,面积有最大值
时,面积有最大值![]() .
.
【解析】
(1)由点C的横坐标为3,代入直线y=![]() x+
x+![]() ,可得点C的坐标为(3,2),再把点C(3,2)代入抛物线,可求得a的值,进而得出抛物线的解析式;
,可得点C的坐标为(3,2),再把点C(3,2)代入抛物线,可求得a的值,进而得出抛物线的解析式;
(2)设点P(m,0),Q(m+1,0),可得点D(m,![]() m+
m+![]() )m,E(m,
)m,E(m,![]() ),G(m+1,
),G(m+1,![]() m+1),F(m+1,
m+1),F(m+1,![]() ),当四边形DEFG为平行四边形时,有ED=FG,可列出关于m的方程,解方程求得m的值,即可得出点P、Q的坐标;
),当四边形DEFG为平行四边形时,有ED=FG,可列出关于m的方程,解方程求得m的值,即可得出点P、Q的坐标;
(3)设以D、E、F、G为顶点的四边形面积为S,由(2)可得,S=![]() ×1÷2=
×1÷2=![]() (﹣m2+m+
(﹣m2+m+![]() )=
)=![]() ,根据二次函数图象的性质即可得出以D、E、F、G为顶点的四边形面积的最大值.
,根据二次函数图象的性质即可得出以D、E、F、G为顶点的四边形面积的最大值.
(1)∵点C的横坐标为3,
∴y=![]() ×3+
×3+![]() =2,
=2,
∴点C的坐标为(3,2),
把点C(3,2)代入抛物线,可得2=9a﹣9a﹣4a,
解得:a=-![]() ,
,
∴抛物线的解析式为y=![]() ;
;
(2)设点P(m,0),Q(m+1,0),
由题意,点D(m,![]() m+
m+![]() )m,E(m,
)m,E(m,![]() ),G(m+1,
),G(m+1,![]() m+1),F(m+1,
m+1),F(m+1,![]() ),
),
∵四边形DEFG为平行四边形,
∴ED=FG,
∴![]() ,即
,即
![]() =
=![]() ,
,
∴m=0.5,
∴P(0.5,0)、Q(1.5,0);
(3)设以D、E、F、G为顶点的四边形面积为S,
由(2)可得,S=![]() ,
,
∴当m=![]() 时,S最大值为
时,S最大值为![]() ,
,
∴以D、E、F、G为顶点的四边形面积有最大值,最大值为![]() .
.