题目内容
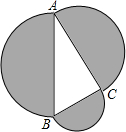如图，分别以直角△ABC的三边AB、BC、CA为直径向外作半圆，设直线AB左边阴影部分面积为S1，右边阴影部分面积为S2，则（ ）| A、S1=S2 | B、S1＜S2 | C、S1＞S2 | D、无法确定 |
分析：因为是直角三角形，所以可以直接运用勾股定理，然后运用圆的面积公式来求解．
解答：解：∵△ABC为直角三角形，
∴AB2=AC2+BC2
又∵S=
πR2
∴S1=
π(
)2=
π•
，S2=
π(
)2+
π(
)2=
π（
）=
π•
=S1
∴S1=S2，
故选A．
∴AB2=AC2+BC2
又∵S=
| 1 |
| 2 |
∴S1=
| 1 |
| 2 |
| AB |
| 2 |
| 1 |
| 2 |
| AB2 |
| 4 |
| 1 |
| 2 |
| AC |
| 2 |
| 1 |
| 2 |
| BC |
| 2 |
| 1 |
| 2 |
| AC2+BC2 |
| 4 |
| 1 |
| 2 |
| AB2 |
| 4 |
∴S1=S2，
故选A．
点评：此题考查的是勾股定理的运用，三角形的直角边之和等于第三边，而且圆的面积公式中R2正好与勾股定理中的平方有联系，因此可将二者结合起来看．
练习册系列答案
海淀课时新作业金榜卷系列答案
期末金牌卷系列答案
轻松课堂标准练系列答案
相关题目
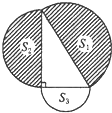如图，分别以直角三角形的三边为直径作半圆，则三个半圆的面积S1，S2+S3之间的关系是（ ）| A、S1＞S2+S3 | B、S1=S2+S3 | C、S1＜S2+S3 | D、无法确定 |
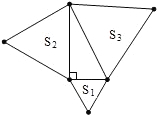如图，分别以直角三角形的三边为边长向外作等边三角形，面积分别记为S1，S2，S3，则S1，S2，S3的关系是（ ）| A、S1+S2=S3 | B、S12+S22=S32 | C、S1+S2＞S3 | D、S1+S2＜S3 |
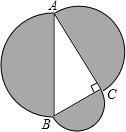如图，分别以直角△ABC的三边AB，BC，CA为直径向外作半圆．设直线AB左边阴影部分的面积为S1，右边阴影部分的面积和为S2，则S1
（2013•攀枝花）如图，分别以直角△ABC的斜边AB，直角边AC为边向△ABC外作等边△ABD和等边△ACE，F为AB的中点，DE与AB交于点G，EF与AC交于点H，∠ACB=90°，∠BAC=30°．给出如下结论：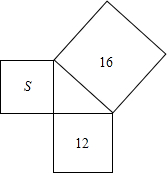
如图，分别以直角三角形三条边为一边向外画三个正方形，则图中字母S所代表的正方形面积为