题目内容

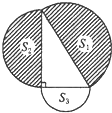如图，分别以直角三角形的三边为直径作半圆，则三个半圆的面积S₁，S₂+S₃之间的关系是（　　）

A、S₁＞S₂+S₃

B、S₁=S₂+S₃

C、S₁＜S₂+S₃

D、无法确定

分析：根据勾股定理以及圆面积公式得，以直角三角形的两条直角边为直径的半圆面积和等于以斜边为直径的半圆面积．

解答：解：设直角三角形的三边分别为a、b、c，
则S₁=

1

2

•π（

c

2

）²=

πc2

8

；
S₂=

1

2

π（

a

2

）²=

πa2

8

；
S₃=

1

2

π（

b

2

）²=

πb2

8

；
S₂+S₃=

πa2

8

+

πb2

8

=

π

8

（a²+b²）=

πc2

8

=S₁．
故选B．

点评：能够熟练运用勾股定理证明此结论．此结论在解题过程中运用可以简便计算，节省时间．

练习册系列答案

全优训练期末测试卷系列答案

新课程成长资源系列答案

新课堂单元测试卷冲刺100分系列答案

学业测评期末考试真题汇编系列答案

名校特优卷系列答案

名校名卷期末冲刺100分系列答案

应用题天天练南海出版公司系列答案

易百分课时训练系列答案

步步高达标卷系列答案

新路学业1课3练课堂学练考系列答案

相关题目

如图，已知矩形OABC，点P在边OA上（不与端点重合），点Q在边CO上（不与端点重合）．
（1）如图（1），若∠BPQ=90°，且△OPQ与△PAB和△QPB相似，请写出表示这三个三角形相似的式子，并探究此时线段OQ、QB、BA之间的数量关系．
（2）若∠PQB=90°，且△OPQ与△PAB、△QPB都相似，如图（2），请重新写出表示这三个三角形相似的式子，并证明AB：OA=2

：3．
（3）在（1）中，若OA=8

CQ．以矩形OABC的两边OA、OC所在的直线分别为x轴和y轴，建立平面直角坐标系，如图（3），若某抛物线顶点为P，点B在抛物线上．
①求此抛物线的解析式．
②过线段BP上一动点M（点M与点P、B不重合），作y轴的平行线交抛物线于点N，若记点M的横坐标为m，试求线段MN的长L与m之间的函数关系式，画出该函数的示意图，并指出m取何值时，L有最大值，最大值是多少？

如图，已知矩形OABC，点P在边OA上（不与端点重合），点Q在边CO上（不与端点重合）．
（1）如图（1），若∠BPQ=90°，且△OPQ与△PAB和△QPB相似，请写出表示这三个三角形相似的式子，并探究此时线段OQ、QB、BA之间的数量关系．
（2）若∠PQB=90°，且△OPQ与△PAB、△QPB都相似，如图（2），请重新写出表示这三个三角形相似的式子，并证明AB：OA=2 $数学公式$ ：3．
（3）在（1）中，若OA=8 $数学公式$ ，OC=8，OP= $数学公式$ CQ．以矩形OABC的两边OA、OC所在的直线分别为x轴和y轴，建立平面直角坐标系，如图（3），若某抛物线顶点为P，点B在抛物线上．
①求此抛物线的解析式．
②过线段BP上一动点M（点M与点P、B不重合），作y轴的平行线交抛物线于点N，若记点M的横坐标为m，试求线段MN的长L与m之间的函数关系式，画出该函数的示意图，并指出m取何值时，L有最大值，最大值是多少？

如图，已知矩形OABC，点P在边OA上（不与端点重合），点Q在边CO上（不与端点重合）．
（1）如图（1），若∠BPQ=90°，且△OPQ与△PAB和△QPB相似，请写出表示这三个三角形相似的式子，并探究此时线段OQ、QB、BA之间的数量关系．
（2）若∠PQB=90°，且△OPQ与△PAB、△QPB都相似，如图（2），请重新写出表示这三个三角形相似的式子，并证明AB：OA=2

：3．
（3）在（1）中，若OA=8

CQ．以矩形OABC的两边OA、OC所在的直线分别为x轴和y轴，建立平面直角坐标系，如图（3），若某抛物线顶点为P，点B在抛物线上．
①求此抛物线的解析式．
②过线段BP上一动点M（点M与点P、B不重合），作y轴的平行线交抛物线于点N，若记点M的横坐标为m，试求线段MN的长L与m之间的函数关系式，画出该函数的示意图，并指出m取何值时，L有最大值，最大值是多少？