题目内容

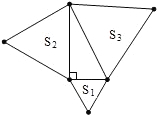精英家教网如图，分别以直角三角形的三边为边长向外作等边三角形，面积分别记为S1，S2，S3，则S1，S2，S3的关系是（　　）
A、S1+S2=S3B、S12+S22=S32C、S1+S2＞S3D、S1+S2＜S3
分析：根据等边三角形的性质，知等边三角形的面积等于其边长的平方的
3
4
倍，结合勾股定理，知以直角三角形的两条直角边为边长的等边三角形的面积和等于以斜边为边长的等边三角形的面积．
解答：解：设直角三角形的三边从小到大是a，b，c．
则S1=
3
4
a2，S2=
3
4
b2，S3=
3
4
c2．
又a2+b2=c2，
则S1+S2=S3．
故选A．
点评：熟悉等边三角形的面积公式，熟练运用勾股定理．
熟记结论：以直角三角形的两条直角边为边长的等边三角形的面积和等于以斜边为边长的等边三角形的面积．
练习册系列答案
相关题目
如图，已知矩形OABC，点P在边OA上（不与端点重合），点Q在边CO上（不与端点重合）．
（1）如图（1），若∠BPQ=90°，且△OPQ与△PAB和△QPB相似，请写出表示这三个三角形相似的式子，并探究此时线段OQ、QB、BA之间的数量关系．
（2）若∠PQB=90°，且△OPQ与△PAB、△QPB都相似，如图（2），请重新写出表示这三个三角形相似的式子，并证明AB：OA=2
3
：3．
（3）在（1）中，若OA=8
2
，OC=8，OP=
2
CQ．以矩形OABC的两边OA、OC所在的直线分别为x轴和y轴，建立平面直角坐标系，如图（3），若某抛物线顶点为P，点B在抛物线上．
①求此抛物线的解析式．
②过线段BP上一动点M（点M与点P、B不重合），作y轴的平行线交抛物线于点N，若记点M的横坐标为m，试求线段MN的长L与m之间的函数关系式，画出该函数的示意图，并指出m取何值时，L有最大值，最大值是多少？

如图，已知矩形OABC，点P在边OA上（不与端点重合），点Q在边CO上（不与端点重合）．
（1）如图（1），若∠BPQ=90°，且△OPQ与△PAB和△QPB相似，请写出表示这三个三角形相似的式子，并探究此时线段OQ、QB、BA之间的数量关系．
（2）若∠PQB=90°，且△OPQ与△PAB、△QPB都相似，如图（2），请重新写出表示这三个三角形相似的式子，并证明AB：OA=2数学公式：3．
（3）在（1）中，若OA=8数学公式，OC=8，OP=数学公式CQ．以矩形OABC的两边OA、OC所在的直线分别为x轴和y轴，建立平面直角坐标系，如图（3），若某抛物线顶点为P，点B在抛物线上．
①求此抛物线的解析式．
②过线段BP上一动点M（点M与点P、B不重合），作y轴的平行线交抛物线于点N，若记点M的横坐标为m，试求线段MN的长L与m之间的函数关系式，画出该函数的示意图，并指出m取何值时，L有最大值，最大值是多少？
如图，已知矩形OABC，点P在边OA上（不与端点重合），点Q在边CO上（不与端点重合）．
（1）如图（1），若∠BPQ=90°，且△OPQ与△PAB和△QPB相似，请写出表示这三个三角形相似的式子，并探究此时线段OQ、QB、BA之间的数量关系．
（2）若∠PQB=90°，且△OPQ与△PAB、△QPB都相似，如图（2），请重新写出表示这三个三角形相似的式子，并证明AB：OA=2：3．
（3）在（1）中，若OA=8，OC=8，OP=CQ．以矩形OABC的两边OA、OC所在的直线分别为x轴和y轴，建立平面直角坐标系，如图（3），若某抛物线顶点为P，点B在抛物线上．
①求此抛物线的解析式．
②过线段BP上一动点M（点M与点P、B不重合），作y轴的平行线交抛物线于点N，若记点M的横坐标为m，试求线段MN的长L与m之间的函数关系式，画出该函数的示意图，并指出m取何值时，L有最大值，最大值是多少？

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网