题目内容
如图所示,在 中,点
中,点 为
为 边上的一点,
边上的一点, .
.
(1)试说明 .
.
(2)求 的长及
的长及 的面积.
的面积.
(2)判断 是否是直角三角形,并说明理由.
是否是直角三角形,并说明理由.
(1)见解析;(2)15,150;(3)是
解析试题分析:(1)根据勾股定理的逆定理即可判断;
(2)先根据勾股定理求得斜边的长,再根据直角三角形的面积公式即可求得结果;
(3)根据勾股定理的逆定理即可判断.
(1)


∴ 是直角三角形
是直角三角形
∴ 即
即 ;
;
(2)∵ ,且点
,且点 为
为 边上的一点
边上的一点
∴
∴由勾股定理得:
∴ ;
;
(3) 是直角三角形
是直角三角形  ,
, 

∴ 是直角三角形.
是直角三角形.
考点:本题考查的是勾股定理,直角三角形的面积公式,勾股定理的逆定理
点评:解答本题的根据是熟练掌握勾股定理的逆定理:如果三角形有两边的平方和等于第三边的平方,那么这个是直角三角形.

练习册系列答案
相关题目
 限速公路上是否超速行驶?(本小问中
限速公路上是否超速行驶?(本小问中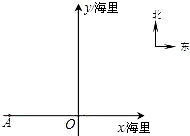 分钟后,渔船行至O处,此时看见小岛B在船的北偏东30°.在如图所示的坐标系中,点O为坐标原点,点A位于x轴上.
分钟后,渔船行至O处,此时看见小岛B在船的北偏东30°.在如图所示的坐标系中,点O为坐标原点,点A位于x轴上. 如图所示,△ABC中,点D在边BC上,点E在边AC上,且AB∥ED,连接BE,若AE:EC=3:5,则下列结论错误的是( )
如图所示,△ABC中,点D在边BC上,点E在边AC上,且AB∥ED,连接BE,若AE:EC=3:5,则下列结论错误的是( ) 中,点
中,点 分别为
分别为 的中点,且
的中点,且 ,则阴影部分的面积为( )。
,则阴影部分的面积为( )。 