题目内容
某段笔直的限速公路上,规定汽车的最高行驶速度不能超过60 km/h(即| 50 |
| 3 |
(1)请在图中画出表示北偏东45°方向的射线AC,并标出点C的位置;
(2)点B坐标为
(3)一辆汽车从点B行驶到点C所用的时间为15 s,请通过计算,判断该汽车在
 限速公路上是否超速行驶?(本小问中
限速公路上是否超速行驶?(本小问中| 3 |
分析:求点的坐标就是求OB、OC的长度,求出BC的长,除以时间就得到汽车的速度,就可以判断是否超速.
解答: 解:(1)如图所示,射线为AC,点C为所求位置;
解:(1)如图所示,射线为AC,点C为所求位置;
(2)在直角三角形ABO中,AO=100,∠BAO=60度,则OB=OA•tan60°=100
,因而点B的坐标是(-100
,0);
直角△AOC是等腰直角三角形,因而OC=OA=100,因而C的坐标是(100,0);
(3)BC=BO+OC=100
+100≈270(m).
270÷15=18(m/s).
∵18>
,
∴这辆车在限速公路上超速行驶了.
 解:(1)如图所示,射线为AC,点C为所求位置;
解:(1)如图所示,射线为AC,点C为所求位置;(2)在直角三角形ABO中,AO=100,∠BAO=60度,则OB=OA•tan60°=100
| 3 |
| 3 |
直角△AOC是等腰直角三角形,因而OC=OA=100,因而C的坐标是(100,0);
(3)BC=BO+OC=100
| 3 |
270÷15=18(m/s).
∵18>
| 50 |
| 3 |
∴这辆车在限速公路上超速行驶了.
点评:解一般三角形,求三角形的边或高的问题一般可以转化为解直角三角形的问题,解决的方法就是作高线.

练习册系列答案
 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案
相关题目
 m/s),交通管理部门在离该公路100m处设置了一速度监测点A,在如图所示的坐标系中,点A位于y轴上,测速路段BC在x轴上,点B在点A的北偏西60°方向上,点C在点A的北偏东45°方向上。
m/s),交通管理部门在离该公路100m处设置了一速度监测点A,在如图所示的坐标系中,点A位于y轴上,测速路段BC在x轴上,点B在点A的北偏西60°方向上,点C在点A的北偏东45°方向上。
 取1.7)
取1.7)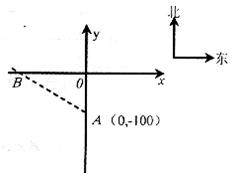
 m/s).交通管理部门在离该公路100 m处设置了一速度监测点A,在如图所示的坐标系中,点A位于y轴上,测速路段BC在x轴上,点B在点A的北偏西60°方向上,点C在点A的北偏东45°方向上.
m/s).交通管理部门在离该公路100 m处设置了一速度监测点A,在如图所示的坐标系中,点A位于y轴上,测速路段BC在x轴上,点B在点A的北偏西60°方向上,点C在点A的北偏东45°方向上. m/s).交通管理部门在离该公路100 m处设置了一速度监测点A,在如图所示的坐标系中,点A位于y轴上,测速路段BC在x轴上,点B在点A的北偏西60°方向上,点C在点A的北偏东45°方向上.
m/s).交通管理部门在离该公路100 m处设置了一速度监测点A,在如图所示的坐标系中,点A位于y轴上,测速路段BC在x轴上,点B在点A的北偏西60°方向上,点C在点A的北偏东45°方向上.