Question

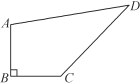
【题目】如图，直角梯形中，，，已知，，动点从点出发，沿线段向点作匀速运动：动点从点出发，沿线段向点作匀速运动．过点垂直于的射线交于点，交于点．、两点同时出发，速度都为每秒个单位长度．当点运动到点，、两点同时停止运动．设点运动的时问为秒．

________，________．（用的代数式表示）；

当为何值时，四边形构成平行四边形？

若为等腰三角形，求的值．

Answer 1

【答案】（1），； ； 当，，时，为等腰三角形．

【解析】

（1）由题意易知四边形ABNQ是矩形，从而可得NC=BC-BN=BC-AQ，由AQ=AD-QD=3-t即可求得NC的长，在Rt△ABC中，利用勾股定理求得AC的长，然后在Rt△MNC中，利用cos∠NCM=，即可求得CM的长；

（2）四边形PCDQ构成平行四边形就是PC=DQ，可得方程4-t=t，解方程即可得；

（3）分三种情况分别进行讨论即可得答案.

由题意易得四边形ABNQ是矩形，

∴BN=AQ，

∵DQ=t，AQ=AD-DQ，

∴，

∴=BC-BN=4-AQ，

在中，，

∴，

在中，，；

由于四边形构成平行四边形，

∴，即，

解得；

①当时（如图），

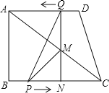
则有：，

即，

∴，

解得：；

②当时（如图），

则有：，

解得：；

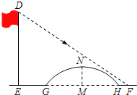
③当时（如图），

在中，

而，，

∴ ，

解得：，（舍去），

∴当，，时，为等腰三角形．