Question

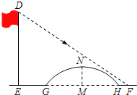
【题目】如图所示，数学小组发现米高旗杆的影子落在了包含一圆弧型小桥在内的路上，于是他们开展了测算小桥所在圆的半径的活动．小刚身高米，测得其影长为米，同时测得的长为米，的长为米，测得小桥拱高（弧的中点到弦的距离，即的长）为米，则小桥所在圆的半径为（ ）

A. B. 5 C. D. 6

Answer 1

【答案】B

【解析】

小桥所在圆的圆心为点O，连结OG，设⊙O的半径为r米．先利用平行投影的性质和相似的性质得到＝，于是可求出GH＝8米，再根据垂径定理得到点O在直线MN上，GM＝HM＝GH＝4米，然后根据勾股定理得到r2＝（r2）2＋16，再解方程即可．

解答：解：如图，设小桥的圆心为O，连接OM、OG．设小桥所在圆的半径为r米．

∵＝，

∴＝

解得EF＝12，

∴GH＝1231＝8（米）．

∵MN为弧GH的中点到弦GH的距离，

∴点O在直线MN上，GM＝HM＝GH＝4米．

在Rt△OGM中，由勾股定理得：OG2＝OM2＋GM2，

即r2＝（r2）2＋16，

解得：r＝5．

答：小桥所在圆的半径为5米．

故选：B．