题目内容
 如图,已知双曲线
如图,已知双曲线 (x<0),经过OABC边AB的中点F,交BC于点E,且四边形OEBF的面积为2,则k为
(x<0),经过OABC边AB的中点F,交BC于点E,且四边形OEBF的面积为2,则k为
- A.2
- B.3
- C.4
- D.-2
D
分析:先求出四边形OEBF的面积和四边形OABC面积的关系,再看△AFO的面积和反比例函数中k的关系,从而确定k的值,可设长方形的长是a,宽是b.
解答: 解:连接OE.
解:连接OE.
设长方形的长是a,宽是b.
所以四边形ABCO的面积是ab.
∵F是中点,
∴AF= ,
,
∴△AFO的面积是 •
• •a=
•a= .
.
∵△AFO的面积=△OCE的面积= =
= .
.
∴四边形OEBF的面积=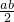 =2.
=2.
∴k=-2.
故选D.
点评:本题考查反比例函数的综合运用,关键是找到三角形的面积和k的关系,以及三角形的面积和四边形面积的关系.
分析:先求出四边形OEBF的面积和四边形OABC面积的关系,再看△AFO的面积和反比例函数中k的关系,从而确定k的值,可设长方形的长是a,宽是b.
解答:
 解:连接OE.
解:连接OE.设长方形的长是a,宽是b.
所以四边形ABCO的面积是ab.
∵F是中点,
∴AF=
 ,
,∴△AFO的面积是
 •
• •a=
•a= .
.∵△AFO的面积=△OCE的面积=
 =
= .
.∴四边形OEBF的面积=
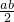 =2.
=2.∴k=-2.
故选D.
点评:本题考查反比例函数的综合运用,关键是找到三角形的面积和k的关系,以及三角形的面积和四边形面积的关系.

练习册系列答案
相关题目
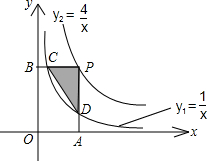 如图,已知双曲线
如图,已知双曲线 (2012•济南)如图,已知双曲线y=
(2012•济南)如图,已知双曲线y= (2013•徐州模拟)如图,已知双曲线y=
(2013•徐州模拟)如图,已知双曲线y= 如图,已知双曲线
如图,已知双曲线 如图,已知双曲线
如图,已知双曲线