题目内容
 如图,已知双曲线y=
如图,已知双曲线y=| 3 |
| x |
| 25 |
| 3 |
| 25 |
| 3 |
分析:过D点作DE⊥OA,DF⊥OC,垂足为E、F,由双曲线的解析式可知S矩形OEDF=3,由于D点在矩形的对角线OB上,可知矩形OEDF∽矩形OABC,可求相似比为0D:OB=3:5,由相似多边形的面积比等于相似比的平方求解.
解答: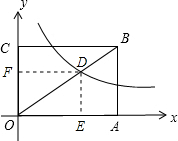 解:过D点作DE⊥OA,DF⊥OC,垂足为E、F,
解:过D点作DE⊥OA,DF⊥OC,垂足为E、F,
∵D点在双曲线y=
上,
∴S矩形OEDF=xy=3,
又∵DB:OD=2:3,
∴0D:OB=3:5,
∵D点在矩形的对角线OB上,
∴矩形OEDF∽矩形OABC,
∴
=(
)2=
,
解得S矩形OABC=3×
=
.
故答案为:
.
 解:过D点作DE⊥OA,DF⊥OC,垂足为E、F,
解:过D点作DE⊥OA,DF⊥OC,垂足为E、F,∵D点在双曲线y=
| 3 |
| x |
∴S矩形OEDF=xy=3,
又∵DB:OD=2:3,
∴0D:OB=3:5,
∵D点在矩形的对角线OB上,
∴矩形OEDF∽矩形OABC,
∴
| S矩形OEDF |
| S矩形OABC |
| OD |
| OB |
| 9 |
| 25 |
解得S矩形OABC=3×
| 25 |
| 9 |
| 25 |
| 3 |
故答案为:
| 25 |
| 3 |
点评:本题考查了反比例函数的综合运用.关键是过D点作坐标轴的垂线,构造矩形,得出其面积为反比例函数的系数的绝对值,再根据多边形的相似中面积的性质求面积.

练习册系列答案
 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案
相关题目
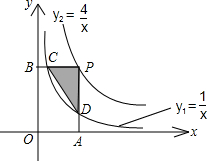 如图,已知双曲线
如图,已知双曲线 (2012•济南)如图,已知双曲线y=
(2012•济南)如图,已知双曲线y= (2013•徐州模拟)如图,已知双曲线y=
(2013•徐州模拟)如图,已知双曲线y= 如图,已知双曲线
如图,已知双曲线