Question

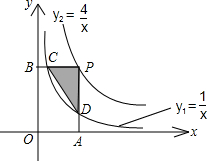
如图，已知双曲线y=

k

x

与直角三角形OAB的斜边OB相交于D，与直角边AB相交于C．若BC：CA=2：1，△OAB的面积为8，则△OED的面积为（　　）

• A．

  4

  3

• B．2
• C．

  8

  3

• D．4

Answer 1

分析：根据等高的三角形面积比等于底的比，求出S_△COA=8×

1

3

=

8

3

，再根据比例系数k的几何意义可得S_△OED和S_△COA都等于

1

2

|k|，可求出△OED的面积．

解答：解：∵△BOC的BC边上的高为AO，△COA的AC边上的高为AO，
又∵BC：CA=2：1，
∴S_△BOC：S_△COA=2：1，
∴S_△COA=8×

1

3

=

8

3

．
∵依据比例系数k的几何意义可得两个三角形的面积都等于

1

2

|k|，
∴S_△OED=S_△COA=

8

3

．
故选C．

点评：本题考查反比例系数k的几何意义，过双曲线上的任意一点分别向两条坐标作垂线，与坐标轴围成的矩形面积就等于|k|．该知识点是中考的重要考点，同学们应高度关注．