题目内容
13．下列方程没有实数根的是（ ）| A． | x2+4x=0 | B． | x2+x-1=0 | C． | x2-2x+3=0 | D． | （x-2）（x-3）=12 |
分析 根据根的判别式△=b2-4ac，逐一分析四个选项中方程根的判别式的符号，由此即可得出结论．
解答 解：A、在方程x2+4x=0中，△=42=16＞0，
∴该方程有两个不相等的实数根；
B、在方程x2+x-1=0中，△=12-4×1×（-1）=5＞0，
∴该方程有两个不相等的实数根；
C、在方程x2-2x+3=0中，△=（-2）2-4×1×3=-8＜0，
∴该方程没有实数根；
D、方程（x-2）（x-3）=12可变形为x2-5x-6=0，△=（-5）2-4×1×（-6）=49＞0，
∴该方程有两个不相等的实数根．
故选C．
点评 本题考查了根的判别式，熟练掌握根的判别式的符号与方程解的个数之间的关系是解题的关键．
练习册系列答案
相关题目
1．
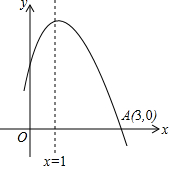如图是二次函数y=ax2+bx+c图象的一部分，且过点A （3，0），二次函数图象的对称轴是x=1．下列结论：①b2＞4ac；②ac＞0； ③a-b+c＞0； ④4a+2b+c＜0．其中错误的结论有（ ）
如图是二次函数y=ax2+bx+c图象的一部分，且过点A （3，0），二次函数图象的对称轴是x=1．下列结论：①b2＞4ac；②ac＞0； ③a-b+c＞0； ④4a+2b+c＜0．其中错误的结论有（ ）| A． | 1个 | B． | 2个 | C． | 3个 | D． | 4个 |
18．二次函数y=ax2+bx+c（a≠0）对于x的任何值都恒为负值的条件是（ ）
| A． | a＞0，?△＞0 | B． | a＞0，?△＜0 | C． | a＜0，?△＞0 | D． | a＜0，?△＜0 |
5．下列方程中是关于x的一元二次方程的是（ ）
| A． | x2+$\frac{1}{{x}^{2}}$=0 | B． | （x-1）（x+2）=1 | C． | ax2+bx+c=0 | D． | x2-2x-3 |
2．在下列各数-$\frac{22}{7}$，0，1.5，-3，5$\frac{1}{2}$，50%，+8中，是整数的有（ ）
| A． | 5个 | B． | 4个 | C． | 3个 | D． | 2个 |
3．
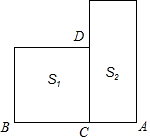如图，若S1表示以BC为边的正方形面积，S2表示以AB为长、AC为宽的矩形面积，且S1=S2．则图中可看作线段黄金分割点的是（ ）
如图，若S1表示以BC为边的正方形面积，S2表示以AB为长、AC为宽的矩形面积，且S1=S2．则图中可看作线段黄金分割点的是（ ）| A． | 点C | B． | 点D | C． | 点C和点D | D． | 没有 |