题目内容
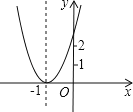
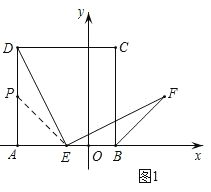
【题目】在平面直角坐标系xOy中，点A（﹣3，0），点B是x轴上异于点A一动点，设B（x，0），以AB为边在x轴的上方作正方形ABCD．
（1）如图（1），若点B（1，0），则点D的坐标为 ；
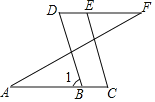
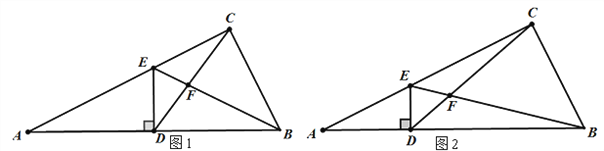
（2）若点E是AB的中点，∠DEF＝90°，且EF交正方形外角的平分线BF于F．
①如图（2），当x＞0时，求证：DE＝EF；
②若点F的纵坐标为y，求y关于x的函数解析式．
【答案】（1）（﹣3，4）；（2）①见解析；②y＝
x+
或y＝﹣x﹣．
【解析】
（1）通过
，
坐标求出正方形的边长，得到
的长，即可写出点
的坐标；
（2）①取中点
，连接
，证
与
全等即可；
②分点在点的右侧和左侧两种情况讨论，先证
与
全等，可得点F的纵坐标为y为
的长度，由
，
，求出含
的代数式的的长度，使其等于
即可．
（1）解：
，
，
，
四边形
为正方形，
，
，
故答案为：
；
（2）①证明：如图1，取中点，连接，
得，
，
四边形是正方形，
，
，
是
中点，
，
，
，
，
是正方形外角的平分线，
，
，
，
，
，
又
，
，
，
；
②如图2，当点在点的右侧时，过点
作
轴于点
，
，
，
，
，
，
；
如图3，当点在点的左侧时，
过点作轴于，
同理可证
，
，
；
关于的函数解析式为
或
．
练习册系列答案
相关题目
