Question

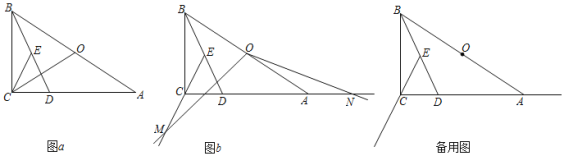
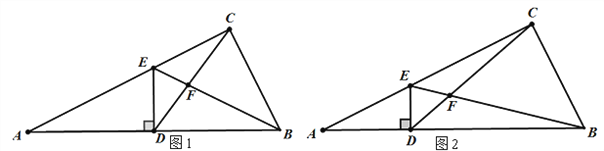
【题目】如图1，点D为直角三角形ABC的斜边AB上的中点，DE⊥AB交AC于E, 连EB、CD，线段CD与BF交于点F.若tanA=,则=_____.如图2，点D为直角三角形ABC的斜边AB上的一点，DE⊥AB交AC于E, 连EB、CD；线段CD与BF交于点F.若，tanA=，则=____.

Answer 1

【答案】

【解析】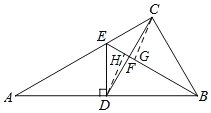

设AC=8a，∵DE⊥AB，tanA═，

∴DE=AD，

∵Rt△ABC中,AC═a，,tanA═，

∴BC=,AB== ，

又∵△AED沿DE翻折，A恰好与B重合，

∴AD=BD= ,DE= ，

∴Rt△ADE中,AE== ，

∴CE=8a-5a=3a，

∴Rt△BCE中,BE==5a，

如图，过点C作CG⊥BE于G，作DH⊥BE于H，则

Rt△BDE中,DH==2a，

Rt△BCE中,CG== ，

∵CG∥DH，

∴△CFG∽△DFH，

∴，

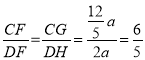故答案为：6：5.

（2）若，tanA=，

∴AD= , BD= ，DE= ，

∴Rt△ADE中,AE== ，

∴CE=8a- = ，

∴Rt△BCE中,BE== ，

如图，过点C作CG⊥BE于G，作DH⊥BE于H，则

Rt△BDE中,DH== ，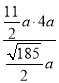

Rt△BCE中,CG== ，

∵CG∥DH，

∴△CFG∽△DFH，

∴，

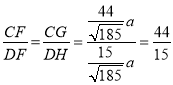故答案为：44：15.