题目内容
【题目】已知等边△ABC的两个顶点坐标为A（-3，0），B（3，0），则点
的坐标为____，△ABC的面积为____．
【答案】(0，
)或(0，-) 
【解析】
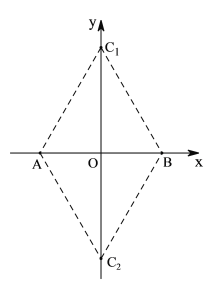
根据A、B坐标及等边三角形的性质可得点C在y轴上，如图，当点C在y轴正半轴时，由AC1=AB=6，OA=3，利用勾股定理求出OC1的长即可得点C1坐标；同理可求出点C在y轴负半轴时C2的坐标；根据S△ABC=
AB·OC即可求出△ABC的面积．
∵A（-3，0），B（3，0），
∴AB中点为（0，0），AB=6，
∵△ABC是等边三角形，
∴点C在y轴上，AC=AB=6，OA=3，
如图，当点C在y轴正半轴时，
OC1=
=3
，
∴C1（0，3），
当点C在y轴负半轴时，
同理可得：OC2=3，
∴C2（0，-3），
综上所述：点C坐标为（0，3）或（0，-3），
∴S△ABC=AB·OC=9，
故答案为：（0，3）或（0，-3）；9
练习册系列答案
相关题目
