题目内容
2. 如图,已知二次函数y=ax2+bx+c(a≠0)的图象与x轴交于点A(-1,0),对称轴为直线x=1,与y轴的交点B在(0,2)和(0,3)之间(包括这两点),下列结论:①当x>3时,y<0;②a-b+c=0;③-1≤a≤-$\frac{2}{3}$;④4a+2b+c<2;其中正确的结论是( )
如图,已知二次函数y=ax2+bx+c(a≠0)的图象与x轴交于点A(-1,0),对称轴为直线x=1,与y轴的交点B在(0,2)和(0,3)之间(包括这两点),下列结论:①当x>3时,y<0;②a-b+c=0;③-1≤a≤-$\frac{2}{3}$;④4a+2b+c<2;其中正确的结论是( )| A. | ①③④ | B. | ①②③ | C. | ①②④ | D. | ①②③④ |
分析 ①先由抛物线的对称性求得抛物线与x轴令一个交点的坐标为(3,0),从而可知当x>3时,y<0;②由抛物线与x轴交于点A(-1,0)可知a-b+c=0,③设抛物线的解析式为y=a(x+1)(x-3),则y=ax2-2ax-3a,令x=0得:y=-3a.由抛物线与y轴的交点B在(0,2)和(0,3)之间,可知2≤-3a≤3.④由抛物线与x轴的交点为(-1,0)和(3,0),且开口向下,根据图象可知当x=2时,y=4a+2b+c>0.
解答 解:①由抛物线的对称性可求得抛物线与x轴令一个交点的坐标为(3,0),当x>3时,y<0,故①正确;
②∵二次函数y=ax2+bx+c(a≠0)的图象与x轴交于点A(-1,0),
∴当x=-1时,y=a-b+c=0,故②正确;
③设抛物线的解析式为y=a(x+1)(x-3),则y=ax2-2ax-3a,
令x=0得:y=-3a.
∵抛物线与y轴的交点B在(0,2)和(0,3)之间,
∴2≤-3a≤3.
解得:-1≤a≤-$\frac{2}{3}$,故③正确;
④∵抛物线与x轴的交点为(-1,0)和(3,0),且开口向下,
∴当x=2时,y=4a+2b+c>0,故④错误.
故选:B.
点评 本题主要考查的是二次函数的图象和性质,掌握抛物线的对称轴、开口方向与系数a、b、c之间的关系是解题的关键.

练习册系列答案
 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案
相关题目
10.2014年云南热带经济作物种植面积3112万亩,2012年种植面积为2845万亩,若从2012到2014年种植面积的平均增长率相同,设平均增长率为x,则下列方程正确的是( )
| A. | 2012(1+x)2=2014 | B. | 2845(1+x)2=3112 | C. | 3112(1+x)2=2845 | D. | 2845(1-x)2=3112 |
17.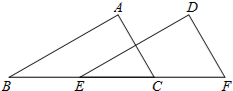 如图,B,C,E,F四点在一条直线上,AB∥DE,AB=DE,下列条件不能判定△ABC与△DEF全等的是( )
如图,B,C,E,F四点在一条直线上,AB∥DE,AB=DE,下列条件不能判定△ABC与△DEF全等的是( )
 如图,B,C,E,F四点在一条直线上,AB∥DE,AB=DE,下列条件不能判定△ABC与△DEF全等的是( )
如图,B,C,E,F四点在一条直线上,AB∥DE,AB=DE,下列条件不能判定△ABC与△DEF全等的是( )| A. | BE=CF | B. | AC=DF | C. | AC∥DF | D. | ∠A=∠D |
7.下列说法正确的是( )
| A. | 三点确定一个圆 | |
| B. | 平分弦的直径垂直于弦,并且平分弦所对的两条弧 | |
| C. | 与直径垂直的直线是圆的切线 | |
| D. | 能够互相重合的弧是等弧 |
14.某旅行社为吸引市民组团去某景区旅游,推出如下收费标准:
某单位组织员工去该风景区旅游,设有x人参加,应付旅游费y元.
(1)请写出y与x的函数关系式;
(2)若该单位现有36人,本次旅游至少去31人,则该单位最多应付旅游费多少元?
| 人数 | 不超过30人 | 超过30人但不超过40人 | 超过40人 |
| 人均旅游费 | 1000元 | 每增加1人,人均旅游费降低20元 | 800元 |
(1)请写出y与x的函数关系式;
(2)若该单位现有36人,本次旅游至少去31人,则该单位最多应付旅游费多少元?