Question

11．如图，经过点A（0，-2）的抛物线y=$\frac{1}{2}$x²+bx+c与x轴相交于点B（-1，0）和C，D为第四象限内抛物线上一点．
（1）求抛物线的解析式；
（2）过点D作y轴的平行线交AC于点E，若AD=AE，求点D的坐标；
（3）连接BD交AC于点F，求$\frac{DF}{BF}$的最大值．

Answer 1

分析 （1）由A、B点在抛物线上，将其代入抛物线方程，即可得出b、c的值，从而得出结论；
（2）过A点作AH⊥DE，垂足为H，设出D点坐标（m，$\frac{1}{2}$m²-$\frac{3}{2}$m-2），用含m的代数式表示出E点坐标，由AD=AE，可得知H点坐标，根据DH=EH即可算出m值，从而得到D点坐标；
（3）借用相似三角形的相似比，可用含m的代数式表示出来$\frac{DF}{BF}$，再按极值问题处理即可得出结论．

解答 解：（1）∵点A（0，-2）和点B（-1，0）均在抛物线上，
∴有$\left\{\begin{array}{l}{c=-2}\\{\frac{1}{2}-b+c=0}\end{array}\right.$，解得$\left\{\begin{array}{l}{b=-\frac{3}{2}}\\{c=-2}\end{array}\right.$，
∴抛物线的解析式为y=$\frac{1}{2}$x²-$\frac{3}{2}$x-2．
（2）过点A作AH⊥DE，垂足为H，如图1．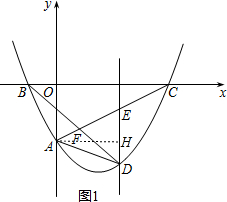

在y=$\frac{1}{2}$x²-$\frac{3}{2}$x-2中，令y=0得，x=-1或x=4，
∴点C坐标为（4，0）．
∵点A坐标为（0，-2），
∴直线AC的解析式为y=$\frac{1}{2}$x-2．
设点D坐标为（m，$\frac{1}{2}$m²-$\frac{3}{2}$m-2），
则点E坐标为（m，$\frac{1}{2}$m-2），点H坐标为（m，-2）．
∵AD=AE，AH⊥DE，
∴DH=HE，即-2-（$\frac{1}{2}$m²-$\frac{3}{2}$m-2）=$\frac{1}{2}$m-2-（-2），
解得m₁=2，m₂=0（不合题意，舍去）．
此时，$\frac{1}{2}$m²-$\frac{3}{2}$m-2=-3，
∴点D的坐标为（2，-3）．
（3）过点D作DG⊥AC，垂足为G，连接AB，DE交x轴于点P，如图2．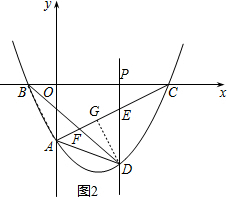

由（2）得，DE=-$\frac{1}{2}$m²+2m．
∵点A（0，-2），点B（-1，0），点O（0，0），点C（4，0），
∴AB=$\sqrt{5}$，AC=2$\sqrt{5}$，BC=5，OC=4，OA=2．
∵DE∥y轴，DG⊥AC，
∴∠DGE=∠CPE=90°，
∵∠DEG=∠CEP（对顶角），
∴∠EDG=∠ECP=∠ACO．
又∵∠DGE=∠COA=90°，
∴△DGE∽△COA，
∴$\frac{DG}{DE}$=$\frac{CO}{CA}$=$\frac{4}{2\sqrt{5}}$=$\frac{2\sqrt{5}}{5}$，
∴DG=$\frac{{2\sqrt{5}}}{5}$DE=$\frac{{2\sqrt{5}}}{5}$（-$\frac{1}{2}$m²+2m）=-$\frac{\sqrt{5}}{5}$（m²-4m）．
∵AB=$\sqrt{5}$，AC=2$\sqrt{5}$，BC=5，
∴AB²+AC²=BC²，
∴∠BAC=90°，
又∵∠DFG=∠BFA，
∴△DGF∽△BAF．
∴$\frac{DF}{BF}$=$\frac{DG}{AB}$=-$\frac{1}{5}$（m²-4m）=-$\frac{1}{5}$（m-2）²+$\frac{4}{5}$．
∴$\frac{DF}{BF}$的最大值为$\frac{4}{5}$．

点评 本题考查了二次函数的综合运用以及相似三角形的判定与性质，解题的关键：（1）代入点的坐标求出b、c；（2）设出D点坐标（m，$\frac{1}{2}$m²-$\frac{3}{2}$m-2），借用线段间的相等关系求出m；（3）借助相似三角形的对应边比等于相似比得出含m的代数式，利用求极值方法得出结论．