题目内容
17.如图,等腰Rt△ABC中,∠BAC=90°,AB=AC,已知A(0,2)、C(5,0).(1)如图①,求点B的坐标;
(2)如图②,BF在△ABC的内部且过B点的任意一条射线,过A作AM⊥BF于M,过C作CN⊥BF于N点,写出BN-NC与AM之间的数量关系,并证明你的结论.
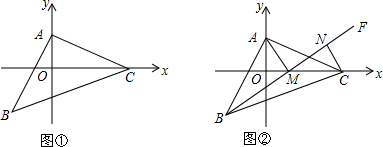
分析 (1)作BD⊥y轴,根据AAS可证明△ABD≌△COA,则BD=OA,AD=OC,即可求出点B的坐标;
(2)BN-NC=2AM,如图②,在BN上截取BG=CN,连接AG,AN,证明△ABG≌△ANC,得到AN=AG,∠CAN=∠BAG,再证明GN=2AM,所以BN-NC=BN-BG=GN=2AM.
解答 解:(1)如图1,作BD⊥y轴,
∵△ABC是等腰直角三角形,∠BAC=90°,
∴AB=AC,∠BAD+∠OAC=90°,
∵∠OCA+∠OAC=90°,
∴∠BAD=∠OCA,
在△ABD和△COA中
$\left\{\begin{array}{l}{∠BDA=∠AOC=9{0}^{°}}\\{∠BAD=∠OCA}\\{AB=AC}\end{array}\right.$,
∴△ABD≌△COA(AAS),
∴OA=BD,OC=AD,
∵A(0,2),C(5,0),
∴OA=2,OC=5,
∴BD=2,AD=5,
∴BD=2,OD=3,
∴B(-2,-3).
(2)BN-NC=2AM,
如图②,在BN上截取BG=CN,连接AG,AN,
∵∠BAC=∠ANC=90°,
∴B,A,N,C四点共圆,
∴∠ANB=∠ACB=45°,∠ACN=∠ABN,
在△ABG和△ANC中,
$\left\{\begin{array}{l}{BG=CN}\\{∠ACN=∠ABN}\\{AC=AB}\end{array}\right.$
∴△ABG≌△ANC,
∴AN=AG,∠CAN=∠BAG,
∵∠ANB=45°,
∴∠ANC=135°,
∴∠NAC+∠ACN=45°,
∴∠ABM+∠BAG=45°,
∴∠AGN=∠ANB=45°,
∴AG=AN,∠GAN=90,且AM⊥MN,
∴AM=MN=MG,
∴GN=2AM,
∴BN-NC=BN-BG=GN=2AM.
点评 本题考查了全等三角形的性质与判定定理,解决本题的关键是△ABD≌△COA,△ABG≌△ANC.

 如图,AB、CD相交于点E.若△AEC≌△BED,则下列结论中不正确的是( )
如图,AB、CD相交于点E.若△AEC≌△BED,则下列结论中不正确的是( )| A. | AC=BD | B. | AC∥BD | C. | E为CD中点 | D. | ∠A=∠D |
| A. | x=3 | B. | x=4 | C. | x=-3 | D. | x=-4 |
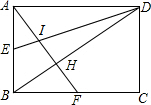 如图,已知矩形ABCD,AB=6,BC=8,E,F分别是AB,BC的中点,AF与DE相交于I,与BD相交于H,则四边形BEIH的面积为( )
如图,已知矩形ABCD,AB=6,BC=8,E,F分别是AB,BC的中点,AF与DE相交于I,与BD相交于H,则四边形BEIH的面积为( )| A. | $\frac{38}{5}$ | B. | $\frac{28}{13}$ | C. | $\frac{28}{5}$ | D. | $\frac{48}{13}$ |
 如图,经过点A(0,-2)的抛物线y=$\frac{1}{2}$x2+bx+c与x轴相交于点B(-1,0)和C,D为第四象限内抛物线上一点.
如图,经过点A(0,-2)的抛物线y=$\frac{1}{2}$x2+bx+c与x轴相交于点B(-1,0)和C,D为第四象限内抛物线上一点. 如图,抛物线y=-x2+ax+8(a≠0)于x轴从左到右交于点A,B于y轴交于点C于直线y=kx+b交于点c和点D(m,5),tan∠DCO=1
如图,抛物线y=-x2+ax+8(a≠0)于x轴从左到右交于点A,B于y轴交于点C于直线y=kx+b交于点c和点D(m,5),tan∠DCO=1 如图,△ABC和△CDE都是等边三角形,试说明∠AEB-∠EBD=60°.
如图,△ABC和△CDE都是等边三角形,试说明∠AEB-∠EBD=60°. △ABC为等边三角形,G,H分别从C,A出发,以等速沿CA,AB运动,连CH,BG交于F.
△ABC为等边三角形,G,H分别从C,A出发,以等速沿CA,AB运动,连CH,BG交于F. 如图,已知CD,BE相交于点A,M是BC的中点,∠1=∠2,∠3=∠4,求证:BD=EC.
如图,已知CD,BE相交于点A,M是BC的中点,∠1=∠2,∠3=∠4,求证:BD=EC.