题目内容
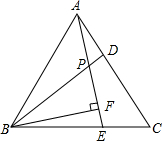 如图,△ABC为等边三角形,D、E分别是AC、BC上的点,且AD=CE,AE与BD相交于点P,BF⊥AE于点F,BP=8,则PF=
如图,△ABC为等边三角形,D、E分别是AC、BC上的点,且AD=CE,AE与BD相交于点P,BF⊥AE于点F,BP=8,则PF=考点:全等三角形的判定与性质,等边三角形的性质,含30度角的直角三角形
专题:
分析:根据等边三角形的性质可得AC=BC,∠BAD=∠C=60°,然后利用“边角边”证明△ABD和△CAE全等,根据全等三角形对应角相等可得∠ABD=∠CAE,然后求出∠BPF=∠BAC=60°,再根据直角三角形两锐角互余求出∠PBF=30°,然后根据直角三角形30°角所对的直角边等于斜边的一半解答.
解答:解:∵△ABC为等边三角形,
∴AC=BC,∠BAD=∠C=60°,
在△ABD和△CAE中,
,
∴△ABD≌△CAE(SAS),
∴∠ABD=∠CAE,
∴∠BPF=∠BAP+∠ABD=∠BAP+∠CAE=∠BAC=60°,
∵BF⊥AE,
∴∠BFP=90°,
∴∠PBF=90°-60°=30°,
∴PF=
BP=
×8=4.
故答案为:4.
∴AC=BC,∠BAD=∠C=60°,
在△ABD和△CAE中,
|
∴△ABD≌△CAE(SAS),
∴∠ABD=∠CAE,
∴∠BPF=∠BAP+∠ABD=∠BAP+∠CAE=∠BAC=60°,
∵BF⊥AE,
∴∠BFP=90°,
∴∠PBF=90°-60°=30°,
∴PF=
| 1 |
| 2 |
| 1 |
| 2 |
故答案为:4.
点评:本题考查了全等三角形的判定与性质,等边三角形的性质,直角三角形30°角所对的直角边等于斜边的一半,熟记各性质并确定出全等三角形,然后求出∠BPF=60°是解题的关键.

练习册系列答案
相关题目
下列线段不能组成直角三角形的是( )
| A、a=6,b=8,c=10 | ||||
| B、a=1,b=2,c=6 | ||||
C、a=
| ||||
| D、a=3,b=4,c=5 |
(a3•a5x)m=a56,当x=5时,m等于( )
| A、29 | B、3 | C、2 | D、5 |
某地一天早晨气温是-3℃,中午上升了12℃,午夜又下降了7℃,则午夜气温是( )
| A、3℃ | B、-3℃ |
| C、2℃ | D、-2℃ |