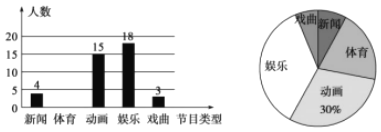
题目内容
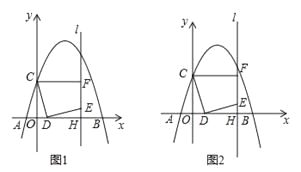
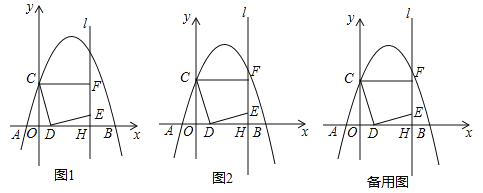
【题目】如图1,在平面直角坐标系中,抛物线![]() 交x轴于A(﹣1,0)和B(5,0)两点,交y轴于点C,点D是线段OB上一动点,连接CD,将线段CD绕点D顺时针旋转90°得到线段DE,过点E作直线l⊥x轴于H,过点C作CF⊥l于F.
交x轴于A(﹣1,0)和B(5,0)两点,交y轴于点C,点D是线段OB上一动点,连接CD,将线段CD绕点D顺时针旋转90°得到线段DE,过点E作直线l⊥x轴于H,过点C作CF⊥l于F.
(1)求抛物线解析式;
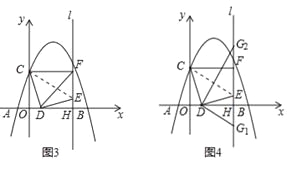
(2)如图2,当点F恰好在抛物线上时,求线段OD的长;
(3)在(2)的条件下:
①连接DF,求tan∠FDE的值;
②试探究在直线l上,是否存在点G,使∠EDG=45°?若存在,请直接写出点G的坐标;若不存在,请说明理由.
【答案】(1)![]() ;(2)1;(3)①
;(2)1;(3)①![]() ;②G(4,
;②G(4,![]() )或(4,6).
)或(4,6).
【解析】
(1)把A、B的坐标代入抛物线的解析式,解方程组即可;
(2)由C的纵坐标求得F的坐标,由△OCD≌△HDE,得出DH=OC=3,即可求得OD的长;
(3)①先确定C、D、E、F四点共圆,由圆周角定理求得∠ECF=∠EDF,由tan∠ECF=![]() =
=![]() ,得到tan∠FDE=
,得到tan∠FDE=![]() ;
;
②连接CE,得出△CDE是等腰直角三角形,∠CED=45°,过D点作DG1∥CE,交直线l于G1,过D点作DG2⊥CE,交直线l于G2,则∠EDG1=45°,∠EDG2=45°,求得直线CE的解析式为![]() ,设直线DG1的解析式为
,设直线DG1的解析式为![]() ,设直线DG2的解析式为
,设直线DG2的解析式为![]() ,把D的坐标代入即可求得m、n,从而求得解析式,进而求得G的坐标.
,把D的坐标代入即可求得m、n,从而求得解析式,进而求得G的坐标.
(1)如图1,∵抛物线![]() 交x轴于A(﹣1,0)和B(5,0)两点,∴
交x轴于A(﹣1,0)和B(5,0)两点,∴![]() ,解得:
,解得: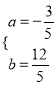 ,∴抛物线解析式为
,∴抛物线解析式为![]() ;
;
(2)如图2,∵点F恰好在抛物线上,C(0,3),∴F的纵坐标为3,把y=3代入![]() 得,
得,![]() ,解得x=0或x=4,∴F(4,3),∴OH=4,∵∠CDE=90°,∴∠ODC+∠EDH=90°,∴∠OCD=∠EDH,在△OCD和△HDE中,∵∠OCD=∠EDH,∠COD=∠DHE=90°,CD=DE,∴△OCD≌△HDE(AAS),∴DH=OC=3,∴OD=4﹣3=1;
,解得x=0或x=4,∴F(4,3),∴OH=4,∵∠CDE=90°,∴∠ODC+∠EDH=90°,∴∠OCD=∠EDH,在△OCD和△HDE中,∵∠OCD=∠EDH,∠COD=∠DHE=90°,CD=DE,∴△OCD≌△HDE(AAS),∴DH=OC=3,∴OD=4﹣3=1;
(3)①如图3,连接CE,∵△OCD≌△HDE,∴HE=OD=1,∵BF=OC=3,∴EF=3﹣1=2,∵∠CDE=∠CFE=90°,∴C、D、E、F四点共圆,∴∠ECF=∠EDF,在RT△CEF中,∵CF=OH=4,∴tan∠ECF=![]() =
=![]() ,∴tan∠FDE=
,∴tan∠FDE=![]() ;
;
②如图4,连接CE,∵CD=DE,∠CDE=90°,∴∠CED=45°,过D点作DG1∥CE,交直线l于G1,过D点作DG2⊥CE,交直线l于G2,则∠EDG1=45°,∠EDG2=45°,∵EH=1,OH=4,∴E(4,1),∵C(0,3),∴直线CE的解析式为![]() ,设直线DG1的解析式为
,设直线DG1的解析式为![]() ,∵D(1,0),∴
,∵D(1,0),∴![]() ,解得m=
,解得m=![]() ,∴直线DG1的解析式为
,∴直线DG1的解析式为![]() ,当x=4时,
,当x=4时,![]() =
=![]() ,∴G1(4,
,∴G1(4,![]() );
);
设直线DG2的解析式为![]() ,∵D(1,0),∴0=2×1+n,解得n=﹣2,∴直线DG2的解析式为
,∵D(1,0),∴0=2×1+n,解得n=﹣2,∴直线DG2的解析式为![]() ,当x=4时,y=2×4﹣2=6,∴G2(4,6);
,当x=4时,y=2×4﹣2=6,∴G2(4,6);
综上,在直线l上,是否存在点G,使∠EDG=45°,点G的坐标为(4,![]() )或(4,6).
)或(4,6).