题目内容
6．
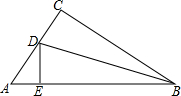如图，在△ABC中，AB=6cm，AC=3cm，BC=5cm，点D、E分别在AC、AB上，且△BCD和△BED关于BD对称，则△ADE的周长为4cm．
分析 先根据△BCD和△BED关于BD对称，得出△BCD≌△BED，故BE=BC，由此可得出AE的长，由△ADE的周长=AE+AD+DE=AE+AC即可得出结论．
解答 解：∵△BCD和△BED关于BD对称，
∴△BCD≌△BED，
∴BE=BC=5cm，
∴AE=6-5=1，
∴△ADE的周长=AE+AD+DE=AE+AC=1+3=4．
故答案为：4．
点评 本题考查的是角平分线的性质，熟知角平分线上的点到角两边的距离相等是解答此题的关键．
练习册系列答案
相关题目
如图，四边形ABCD内接于⊙O，∠A=115°，则∠BOD等于130°．
11．适合下列条件的△ABC中，是直角三角形的个数为（ ）
①a=$\frac{1}{3}$，b=$\frac{1}{4}$，c=$\frac{1}{5}$②∠A-∠B=∠C③∠A=32°，∠B=58°④a=7，b=24，c=25．
①a=$\frac{1}{3}$，b=$\frac{1}{4}$，c=$\frac{1}{5}$②∠A-∠B=∠C③∠A=32°，∠B=58°④a=7，b=24，c=25．
| A． | 1个 | B． | 2个 | C． | 3个 | D． | 4个 |
18．对于实数c，d，我们可用min{c，d}表示c，d两数中较小的数，如min{3，-1}=-1．则关于x的代数式min{3x${\;}^{2}-\frac{3}{2}$，x2+2x+1}的最小值是（ ）
| A． | $\frac{3}{2}$ | B． | -1 | C． | -$\frac{3}{2}$ | D． | -2 |
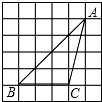在正方形网格中，△ABC如图所示放置在网格中，则tanA=$\frac{3}{5}$．