��Ŀ����
�۲����е�ʽ��
��һ����ʽ��a1=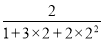 =
=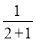 -
-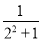
�ڶ�����ʽ��a2= =
=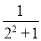 -
-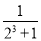
��������ʽ��a3= =
=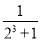 -
-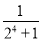
���ĸ���ʽ��a4= =
=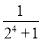 -
-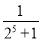
���������ɣ��ش��������⣺
��1����д����������ʽ��a6=_____=_____��
��2���ú�n�Ĵ���ʽ��ʾ��n����ʽ��an=_____=_____��
��3��a1+a2+a3+a4+a5+a6=_____�����������
��4�����㣺a1+a2+��+an��
��1���� -����2���� -����3������4��. ����������1��������֪4����ʽ�ɵã� ��2��������֪��ʽ�ó��𰸣� ��3���������õ�ʽ�Ĺ����г���ʽ��Ȼ���������������㻯������ʽ���ɵã� ��4��������֪��ʽ���ɣ������������ɵã� �������� ��1��������֪��a6==-�� ��2��an==-�� ��3��ԭʽ=��+��+��+��+��+�� =�� =�� ...
��ϰ��ϵ�д�
 �����ҵ���������ϵ�д�
�����ҵ���������ϵ�д� �����̸�Ӯ����ٸ�Ч�����ܸ�ϰ���ϿƼ�������ϵ�д�
�����̸�Ӯ����ٸ�Ч�����ܸ�ϰ���ϿƼ�������ϵ�д� �����ҵ�����������ѧ���ӳ�����ϵ�д�
�����ҵ�����������ѧ���ӳ�����ϵ�д� ����ѧ��Ӯ�����ϵ�д�
����ѧ��Ӯ�����ϵ�д�
�����Ŀ
������һ�����˸���Ϸ̯λ���ο�ֻ����һö���������ӣ��������3�㣬�Ϳɻ�ü�ֵ10Ԫ�Ľ�Ʒ��ÿ����1������ֻ�踶1Ԫ�ķ��ã�С����̯λǰ�۲��˺ܾã��������ο͵��н������
�ο� | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
�������� | 30 | 20 | 25 | 6 | 16 | 50 | 12 |
����� | 1 | 0 | 0 | 1 | 0 | 2 | 0 |
����С���ļ�¼������ʲô������
������. ������������������ȸ������������ӵ��ص�����3���ֵĸ��ʣ�����С��ʵ�ʼ�¼���н�������Ƚϼ��ɵó����ۣ� ����������������� ����һ����ͨ�����������ӣ�3����ֵĸ���ӦΪ�� С����¼����������Ϊ159�Σ��н��Ĵ���ӦΪ27�����ң���ʵ���н�����ֻ��4�Σ����ǿ��Ի��ɰ�̯�����õ����������ֲ������ȣ�Ҫ��һ��֤ʵ���ֻ��ɣ�����ͨ���������������ɣ�

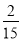 B.
B. 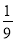 C.
C. 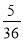 D.
D. 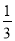
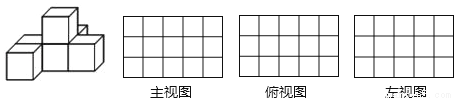
 B.
B. 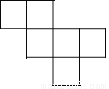 C.
C. 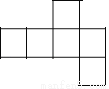 D.
D. 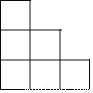

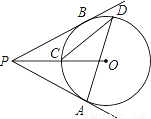
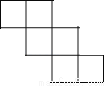
 �ϲ����A����C�غϵ�һ�����㣬����AD��CD������APB=80�㣬���ADC�Ķ����ǣ� ��
�ϲ����A����C�غϵ�һ�����㣬����AD��CD������APB=80�㣬���ADC�Ķ����ǣ� ��