ЬтФПФкШн
ЁОЬтФПЁПШчЭМЃЌвЛДЮКЏЪ§![]() ЕФЭМЯѓгыЖўДЮКЏЪ§
ЕФЭМЯѓгыЖўДЮКЏЪ§![]() ЕФЭМЯѓНЛгкзјБъжсЩЯЕФ
ЕФЭМЯѓНЛгкзјБъжсЩЯЕФ![]() СНЕуЃЎ
СНЕуЃЎ
ЃЈ1ЃЉЧѓЖўДЮКЏЪ§ЕФНтЮіЪНЃЛ
ЃЈ2ЃЉЕу![]() ЪЧжБЯп
ЪЧжБЯп![]() ЩЯЗНХзЮяЯпЩЯвЛЕуЃЌЙ§Еу
ЩЯЗНХзЮяЯпЩЯвЛЕуЃЌЙ§Еу![]() ЗжБ№зї
ЗжБ№зї![]() жс
жс![]() жсЦНааЯпЗжБ№НЛжБЯп
жсЦНааЯпЗжБ№НЛжБЯп![]() гкЕу
гкЕу![]() КЭЕу
КЭЕу![]() ЃЌЩшЕу
ЃЌЩшЕу![]() ЕФКсзјБъЮЊ
ЕФКсзјБъЮЊ![]() ЃЌЧыгУКЌ
ЃЌЧыгУКЌ![]() ЕФДњЪ§ЪНБэЪО
ЕФДњЪ§ЪНБэЪО![]() ЕФжмГЄЃЌВЂЧѓГіЕБ
ЕФжмГЄЃЌВЂЧѓГіЕБ![]() ЕФжмГЄШЁЕУзюДѓжЕ(ВЛашвЊЧѓГіДЫзюДѓжЕ)ЪБЕу
ЕФжмГЄШЁЕУзюДѓжЕ(ВЛашвЊЧѓГіДЫзюДѓжЕ)ЪБЕу![]() ЕФзјБъЃЛ
ЕФзјБъЃЛ
ЃЈ3ЃЉЕу![]() ЪЧжБЯп
ЪЧжБЯп![]() ЩЯвЛЕуЃЌЕу
ЩЯвЛЕуЃЌЕу![]() ЪЧХзЮяЯпЩЯвЛЕуЃЌдкЕкЖўЮЪ
ЪЧХзЮяЯпЩЯвЛЕуЃЌдкЕкЖўЮЪ![]() ЕФжмГЄШЁЕУзюДѓжЕЕФЬѕМўЯТЃЌЧыжБНгаДГіЪЙвдЕу
ЕФжмГЄШЁЕУзюДѓжЕЕФЬѕМўЯТЃЌЧыжБНгаДГіЪЙвдЕу![]() ЮЊЖЅЕуЕФЫФБпаЮЪЧЦНааЫФБпаЮЕФЕу
ЮЊЖЅЕуЕФЫФБпаЮЪЧЦНааЫФБпаЮЕФЕу![]() ЕФзјБъЃЎ
ЕФзјБъЃЎ
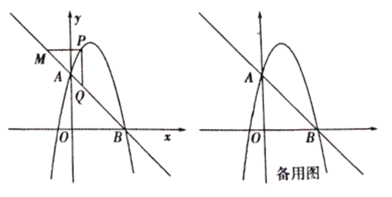
ЁОД№АИЁПЃЈ1ЃЉ![]() ЃЛЃЈ2ЃЉжмГЄ
ЃЛЃЈ2ЃЉжмГЄ![]() ЃЌ
ЃЌ![]() ЃЛЃЈ3ЃЉЕу
ЃЛЃЈ3ЃЉЕу![]() ЕФзјБъЮЊ
ЕФзјБъЮЊ![]() Лђ
Лђ![]()
ЁОНтЮіЁП
ЃЈ1ЃЉЯШРћгУвЛДЮКЏЪ§НтЮіЪНЃЌЧѓГіAЃЌBзјБъЃЌдйДњШы![]() ЃЌЧѓГіbЃЌcМДПЩЕУЕНЖўДЮКЏЪ§НтЮіЪНЃЛ
ЃЌЧѓГіbЃЌcМДПЩЕУЕНЖўДЮКЏЪ§НтЮіЪНЃЛ
ЃЈ2ЃЉЩшЕу![]() ЃЌПЩЕУГіPQЕФБэДяЪНЃЌвзжЄ
ЃЌПЩЕУГіPQЕФБэДяЪНЃЌвзжЄ![]() ЮЊЕШбќжБНЧШ§НЧаЮЃЌМДПЩЕУГі
ЮЊЕШбќжБНЧШ§НЧаЮЃЌМДПЩЕУГі![]() ЃЌдйРћгУЖўДЮКЏЪ§ЕФаджЪПЩЕУГіжмГЄзюДѓЪБMЕФзјБъЃЛ
ЃЌдйРћгУЖўДЮКЏЪ§ЕФаджЪПЩЕУГіжмГЄзюДѓЪБMЕФзјБъЃЛ
ЃЈ3ЃЉЩш![]() ЃЌ
ЃЌ![]() ЃЌИљОнЦНааЫФБпаЮЖдНЧЯпЛЅЯрЦНЗжЕФаджЪЃЌЗжБ№ЬжТлPCЃЌPQЃЌPDЮЊЖдНЧЯпЃЌНЈСЂЗНГЬЧѓНтЃЎ
ЃЌИљОнЦНааЫФБпаЮЖдНЧЯпЛЅЯрЦНЗжЕФаджЪЃЌЗжБ№ЬжТлPCЃЌPQЃЌPDЮЊЖдНЧЯпЃЌНЈСЂЗНГЬЧѓНтЃЎ
НтЃКЃЈ1ЃЉСю![]() жа
жа![]() ЮЊ0ЕУy=4ЃЌдђ
ЮЊ0ЕУy=4ЃЌдђ![]() ЃЌ
ЃЌ
Сюy=0ЃЌЕУ![]() ЃЌНтЕУ
ЃЌНтЕУ![]() ЃЌдђ
ЃЌдђ![]()
ЗжБ№НЋЕу![]() ЕФзјБъДњШЫЕН
ЕФзјБъДњШЫЕН![]() ЃЌ
ЃЌ
ЕУ![]() ЃЌНтЕУ
ЃЌНтЕУ![]()
ЁрЖўДЮКЏЪ§ЕФНтЮіЪНЮЊ![]() ЃЎ
ЃЎ
ЃЈ2ЃЉгЩЬтвтЩшЕу![]() ЃЌ
ЃЌ
дђ![]() ЃЎ
ЃЎ
Ёп![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
Ёп![]() жсЃЌ
жсЃЌ ![]() жсЃЌ
жсЃЌ
Ёр![]() ЃЌМД
ЃЌМД![]() ЮЊЕШбќжБНЧШ§НЧаЮЃЎ
ЮЊЕШбќжБНЧШ§НЧаЮЃЎ
Щш![]() ЕФжмГЄЮЊ
ЕФжмГЄЮЊ![]() ЃЌдђ
ЃЌдђ![]() ЃЌ
ЃЌ
МД![]() ЃЎ
ЃЎ
ЕБ![]() ЪБЃЌ
ЪБЃЌ![]() ЕФжмГЄШЁЕУзюДѓжЕЃЌ
ЕФжмГЄШЁЕУзюДѓжЕЃЌ
НЋ![]() ДњШыЕН
ДњШыЕН![]() жаПЩЕУЃЌ
жаПЩЕУЃЌ![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
Ёп![]() жсЃЌ
жсЃЌ
Ёр![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
Ёр![]()
ЃЈ3ЃЉЩш![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
дкЃЈ2ЃЉЕФЬѕМўЯТPЕузјБъЮЊ![]() ЃЌQЕузјБъЮЊ
ЃЌQЕузјБъЮЊ![]()
ЂйЕБPCЮЊЖдНЧЯпЪБЃЌ
![]() ЃЌНтЕУ
ЃЌНтЕУ![]()
ДЫЪБC![]() гыQЕужиКЯЃЌВЛЗћКЯЬтвтЃЌЩсШЅЃЛ
гыQЕужиКЯЃЌВЛЗћКЯЬтвтЃЌЩсШЅЃЛ
ЂкЕБPQЮЊЖдНЧЯпЪБЃЌ
![]() ЃЌНтЕУ
ЃЌНтЕУ![]()
ДЫЪБC![]() гыQЕужиКЯЃЌВЛЗћКЯЬтвтЃЌЩсШЅЃЛ
гыQЕужиКЯЃЌВЛЗћКЯЬтвтЃЌЩсШЅЃЛ
ЂлЕБPDЮЊЖдНЧЯпЪБЃЌ
![]() ЃЌНтЕУ
ЃЌНтЕУ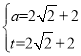 Лђ
Лђ
ЕБ![]() ЪБЃЌ
ЪБЃЌ![]() ЃЌМД
ЃЌМД![]()
ЕБ![]() ЪБЃЌ
ЪБЃЌ![]() ЃЌМД
ЃЌМД![]()
злЩЯЃЌЕу![]() ЕФзјБъЮЊ
ЕФзјБъЮЊ![]() Лђ
Лђ![]() ЃЎ
ЃЎ

 дФЖСПьГЕЯЕСаД№АИ
дФЖСПьГЕЯЕСаД№АИ