Question

【题目】如图，是的直径，点是圆上不与点重合的动点，连接并延长到点，使，点是的中点，连接．

（1）求证：；

（2）填空：①若，当时，四边形是菱形；

②当四边形是正方形时， ________°

Answer 1

【答案】（1）见解析；（2）①5，②45°

【解析】

（1）连接PB，利用直径所对的圆周角是直角，易得PB垂直平分AD，从而得到BA=BD，即可得证；

（2）①根据P为AD中点，C为BD中点，可得PC∥OA，PC=AB=OA，从而判定四边形AOCP为平行四边形，再根据邻边相等的平行四边形为菱形即可的答案；

②由正方形的性质可得∠POB=∠POA=90°，易得△OPA为等腰直角三角形，再利用PC∥AO即可得∠DPC=∠A=45°．

（1）证明：如图，连接

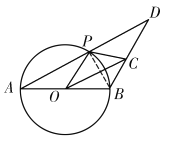
∵是的直径，

，

是线段的垂直平分线，

，

（2）①，

∵是的直径，

，

，

∴四边形是平行四边形

∴当时，平行四边形是菱形．

故答案为：5．

②∵四边形是正方形，

∴∠POB=∠POA=90°

∵

∴

故答案为：45°．