题目内容
14.阅读理解:如图1,在Rt△ABC中,∠C=90°,∠A所对的边BC记为a,叫做∠A的对边,∠A所相邻的边AC记为b,叫做∠A邻边,新定义:tan∠A=$\frac{∠A的对边}{∠A的邻边}$=$\frac{a}{b}$①在Rt△ABC中,∠C=90°,∠A=30°,BC=2,AB=4,则tan30°=$\frac{\sqrt{3}}{3}$,tan60°=$\sqrt{3}$;
②在等腰直角三角形中,则tan45°=1
③运用新知:喜欢数学的小伟沿笔直的河岸BC进行数学实践活动,如图2,河对岸有一码头A,小伟在河岸B处测得
∠ABD=45°,沿河岸行走300米后到达C处,在C处测得∠ACD=30°,求河宽AD.
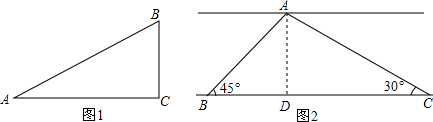
分析 ①根据新定义:tan∠A=$\frac{∠A的对边}{∠A的邻边}$=$\frac{a}{b}$即可求解;
②画出等腰直角三角形ABC,∠C=90°,a=b,根据新定义:tan∠A=$\frac{∠A的对边}{∠A的邻边}$=$\frac{a}{b}$即可求出tan45°的值;
③由图2可知AD⊥BC,于是∠ABD=∠BAD=45°,以及∠ACD=30°,设AD=x,则有BD=x,CD=$\sqrt{3}$x,根据BD+CD=300得出方程x+$\sqrt{3}$x=300,求出即可.
解答 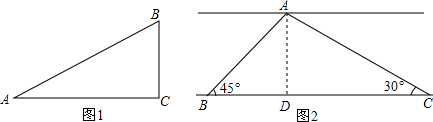 解:①如图1.
解:①如图1.
∵在Rt△ABC中,∠C=90°,BC=2,AB=4,
∴AC=$\sqrt{A{B}^{2}-B{C}^{2}}$=$\sqrt{{4}^{2}-{2}^{2}}$=2$\sqrt{3}$,
∵∠A=30°,
∴tan30°=tan∠A=$\frac{BC}{AC}$=$\frac{2}{2\sqrt{3}}$=$\frac{\sqrt{3}}{3}$,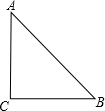 tan60°=tan∠B=$\frac{AC}{BC}$=$\frac{2\sqrt{3}}{2}$=$\sqrt{3}$;
tan60°=tan∠B=$\frac{AC}{BC}$=$\frac{2\sqrt{3}}{2}$=$\sqrt{3}$;
②如右图,在等腰直角三角形ABC中,∠C=90°,AC=BC,
则∠A=∠B=45°,
所以tan45°=tan∠A=$\frac{BC}{AC}$=1;
③由图2可知AD⊥BC,于是∠ABD=∠BAD=45°,∠ACD=30°.
在Rt△ABD中,BD=AD.
在Rt△ACD中,CD=$\sqrt{3}$AD.
设AD=x,则有BD=x,CD=$\sqrt{3}$x.
依题意,得BD+CD=300,
即x+$\sqrt{3}$x=300,
(1+$\sqrt{3}$)x=300,
解得x=150$\sqrt{3}$-150(米).
答:河宽AD为(150$\sqrt{3}$-150)米.
故答案为$\frac{\sqrt{3}}{3}$,$\sqrt{3}$;1.
点评 此题主要考查了解直角三角形的应用,学生的阅读理解能力及知识的迁移能力.正确理解新定义:tan∠A=$\frac{∠A的对边}{∠A的邻边}$=$\frac{a}{b}$是解决本题的关键.

 在如图所示的方格中分别填入-8,-6,-4,-2,2,4,6,8这8个数,使得每行的三个数,每列的三个数,斜对角的三个数之和都相等.
在如图所示的方格中分别填入-8,-6,-4,-2,2,4,6,8这8个数,使得每行的三个数,每列的三个数,斜对角的三个数之和都相等.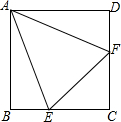 如图所示,在正方形ABCD中,∠EAF=45°,∠EAF绕点A顺时针旋转,它的两边分别交CB,DC(或它们的延长线)于点E、F.当∠EAF绕点A旋转到BE=DF时,连接EF.小明发现BE+DF=EF,你同意他的看法吗?说明理由.
如图所示,在正方形ABCD中,∠EAF=45°,∠EAF绕点A顺时针旋转,它的两边分别交CB,DC(或它们的延长线)于点E、F.当∠EAF绕点A旋转到BE=DF时,连接EF.小明发现BE+DF=EF,你同意他的看法吗?说明理由.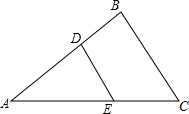 如图,在△ABC中,点D、E分别在AB和AC边上,若$\frac{AB}{AC}$=$\frac{AD}{AE}$=$\frac{4}{5}$,EC=4cm,求线段BD的长.
如图,在△ABC中,点D、E分别在AB和AC边上,若$\frac{AB}{AC}$=$\frac{AD}{AE}$=$\frac{4}{5}$,EC=4cm,求线段BD的长. 如图,在∠AOB内部一找P,使点P到OA和BO的距离相等,且到点O的距离等于2.5厘米,请你在图中找出这个点.
如图,在∠AOB内部一找P,使点P到OA和BO的距离相等,且到点O的距离等于2.5厘米,请你在图中找出这个点.