题目内容
已知菱形的周长为30cm，两个相邻内角的度数之比为1：2，则较短对角线的长为 ．
考点：菱形的性质
专题：
分析：由已知可求得较短的对角线与菱形的一组邻边组成一个等边三角形，从而得到较短的对角线的长等于其边长．
解答：
解：相邻两个内角的度数之比是1：2，
∴两个相邻角度分别为60°、120°，
∵较长的对角线所对的角为120°，
∴较短的对角线所对的角为60°，较短的对角线与菱形的一组邻边构成的是等边三角形，
那么较短的对角线长为30÷4=7.5（cm）．
故答案为：7.5cm．
解：相邻两个内角的度数之比是1：2，∴两个相邻角度分别为60°、120°，
∵较长的对角线所对的角为120°，
∴较短的对角线所对的角为60°，较短的对角线与菱形的一组邻边构成的是等边三角形，
那么较短的对角线长为30÷4=7.5（cm）．
故答案为：7.5cm．
点评：此题主要考查菱形的性质及等边三角形的判定的理解及运用，难度一般，如果不熟练菱形的性质，解答本题的时候可以先画出草图．
练习册系列答案
相关题目
如图，作字母N（折线ABCD）关于y轴的轴对称图形，并写出所得图形相对应的坐标．
如图，在△ABC中，AD是高，DE分别在AB、AC上，DE∥BC，∠ADE=50°，∠C=70°，求∠A的大小？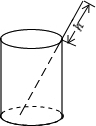
如图，将一根长12厘米的筷子置于底面直径为6厘米，高为8厘米的圆柱形杯子中，则筷子露在杯子外面的长度至少为