题目内容
4.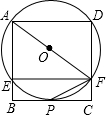 如图,正方形ABCD顶点A,D在⊙O上,边BC经过⊙O上一定P,且PF平分∠AFC,边 AB,CD分别与⊙O相交于点E、F,连接EF.
如图,正方形ABCD顶点A,D在⊙O上,边BC经过⊙O上一定P,且PF平分∠AFC,边 AB,CD分别与⊙O相交于点E、F,连接EF.(1)求证:BC是⊙O的切线;
(2)若FC=2,求PC的长.
分析 (1)证明:连接OP,
∵四边形ABCD是正方形,
∴∠B=∠C=∠D=90°,AB=BC,
∵PF平分∠AFC,
∴∠AFP=∠PFC,
∵OP=OF,
∴∠AFP=∠OPF,
∴∠PFC=∠OPF,
∴OP∥CD,
∴∠BPO=∠C=90°,
∴OP⊥BC,
∴BC是⊙O的切线;
(2)解:连接AP,∵∠D=90°,∴AF是⊙O的直径,
∴∠AEF=∠APF=90°,
∴∠BEF=∠B=∠C=90°,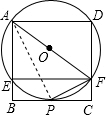
∵OP∥CD,∴OP∥CD∥BA,
∴$\frac{AO}{AF}=\frac{BP}{BC}=\frac{1}{2}$,
∴BP=$\frac{1}{2}$BC=$\frac{1}{2}$BA,
∵∠APB+∠FPC=90°,∠PFC+∠FPC=90°,
∴∠APB=∠PFC,
∵∠B=∠C=90°,
∴△APB∽△PFC,
∴$\frac{FC}{PB}=\frac{CP}{BA}=\frac{1}{2}$,∴$\frac{FC}{CP}=\frac{PB}{BA}=\frac{1}{2}$,
∴PC=2FC=4.
解答 (1)证明:连接OP,
∵四边形ABCD是正方形,
∴∠B=∠C=∠D=90°,AB=BC,
∵PF平分∠AFC,
∴∠AFP=∠PFC,
∵OP=OF,
∴∠AFP=∠OPF,
∴∠PFC=∠OPF,
∴OP∥CD,
∴∠BPO=∠C=90°,
∴OP⊥BC,
∴BC是⊙O的切线;
(2)解:连接AP,∵∠D=90°,∴AF是⊙O的直径,
∴∠AEF=∠APF=90°,
∴∠BEF=∠B=∠C=90°,
∵OP∥CD,∴OP∥CD∥BA,
∴$\frac{AO}{AF}=\frac{BP}{BC}=\frac{1}{2}$,
∴BP=$\frac{1}{2}$BC=$\frac{1}{2}$BA,
∵∠APB+∠FPC=90°,∠PFC+∠FPC=90°,
∴∠APB=∠PFC,
∵∠B=∠C=90°,
∴△APB∽△PFC,
∴$\frac{FC}{PB}=\frac{CP}{BA}=\frac{1}{2}$,∴$\frac{FC}{CP}=\frac{PB}{BA}=\frac{1}{2}$,
∴PC=2FC=4.
点评 本题考查了切线的判定和性质,相似三角形的判定和性质,平行线分线段成比例定理,圆周角定理,正确的作出辅助线是解题的关键.

| A. |  | B. |  | C. |  | D. |  |
 如图,放置的△OAB1,△B1A1B2,△B2A2B3,…都是边长为2的等边三角形,边AO在y轴上,点B1,B2,B3,…都在直线y=$\frac{\sqrt{3}}{3}$x上,则A2017的坐标为( )
如图,放置的△OAB1,△B1A1B2,△B2A2B3,…都是边长为2的等边三角形,边AO在y轴上,点B1,B2,B3,…都在直线y=$\frac{\sqrt{3}}{3}$x上,则A2017的坐标为( )| A. | 2015$\sqrt{3}$,2017 | B. | 2016$\sqrt{3}$,2018 | C. | 2017$\sqrt{3}$,2019 | D. | 2017$\sqrt{3}$,2017 |
| A. | 6 | B. | 7 | C. | 8 | D. | 9 |
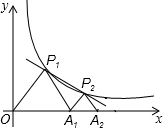 如图,P1、P2(P2在P1的右侧)是y=$\frac{k}{x}$(k>0)在第一象限上的两点,点A1的坐标为(2,0).
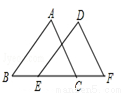
如图,P1、P2(P2在P1的右侧)是y=$\frac{k}{x}$(k>0)在第一象限上的两点,点A1的坐标为(2,0).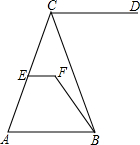 如图,EF∥AB,∠DCB=80°,∠CBF=20°,∠EFB=120°,判断直线CD与AB有怎样的位置关系,并说明理由.
如图,EF∥AB,∠DCB=80°,∠CBF=20°,∠EFB=120°,判断直线CD与AB有怎样的位置关系,并说明理由.