题目内容
6.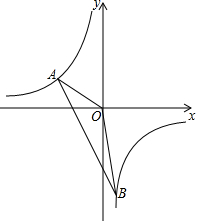 如图,一次函数y=kx+b的图象与反比例函数y=$\frac{m}{x}$的图象交于点A(-3,m+8),B(n,-6)两点.
如图,一次函数y=kx+b的图象与反比例函数y=$\frac{m}{x}$的图象交于点A(-3,m+8),B(n,-6)两点.(1)求一次函数与反比例函数的解析式;
(2)求△AOB的面积.
分析 (1)将点A坐标代入反比例函数求出m的值,从而得到点A的坐标以及反比例函数解析式,再将点B坐标代入反比例函数求出n的值,从而得到点B的坐标,然后利用待定系数法求一次函数解析式求解;
(2)设AB与x轴相交于点C,根据一次函数解析式求出点C的坐标,从而得到点OC的长度,再根据S△AOB=S△AOC+S△BOC列式计算即可得解.
解答 解:(1)将A(-3,m+8)代入反比例函数y=$\frac{m}{x}$得,
$\frac{m}{-3}$=m+8,
解得m=-6,
m+8=-6+8=2,
所以,点A的坐标为(-3,2),
反比例函数解析式为y=-$\frac{6}{x}$,
将点B(n,-6)代入y=-$\frac{6}{x}$得,-$\frac{6}{n}$=-6,
解得n=1,
所以,点B的坐标为(1,-6),
将点A(-3,2),B(1,-6)代入y=kx+b得,
$\left\{\begin{array}{l}{-3k+b=2}\\{k+b=-6}\end{array}\right.$,
解得$\left\{\begin{array}{l}{k=-2}\\{b=-4}\end{array}\right.$,
所以,一次函数解析式为y=-2x-4;
(2)设AB与x轴相交于点C,
令-2x-4=0解得x=-2,
所以,点C的坐标为(-2,0),
所以,OC=2,
S△AOB=S△AOC+S△BOC,
=$\frac{1}{2}$×2×2+$\frac{1}{2}$×2×6,
=2+6,
=8.
点评 本题考查了反比例函数与一次函数交点问题,主要利用了待定系数法求一次函数解析式和待定系数法求反比例函数解析式,三角形的面积的求解,关键在于先求出点A的坐标.

练习册系列答案
相关题目
16. 一个立方体的表面展开图如图所示,将其折叠成立方体后,“你”字对面的字是( )
一个立方体的表面展开图如图所示,将其折叠成立方体后,“你”字对面的字是( )
 一个立方体的表面展开图如图所示,将其折叠成立方体后,“你”字对面的字是( )
一个立方体的表面展开图如图所示,将其折叠成立方体后,“你”字对面的字是( )| A. | 中 | B. | 考 | C. | 顺 | D. | 利 |
17.下列四个图形中,是轴对称图形,但不是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
14.下面的几何体中,主视图为圆的是( )
| A. |  | B. |  | C. |  | D. |  |
8.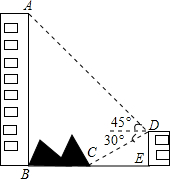 如图,大楼AB的右侧有一障碍物,在障碍物的旁边有一幢小楼DE,在小楼的顶端D处测得障碍物边缘点C的俯角为30°,测得大楼顶端A的仰角为45°(点B,C,E在同一水平直线上).已知AB=80m,DE=10m,求障碍物B,C两点间的距离是( )
如图,大楼AB的右侧有一障碍物,在障碍物的旁边有一幢小楼DE,在小楼的顶端D处测得障碍物边缘点C的俯角为30°,测得大楼顶端A的仰角为45°(点B,C,E在同一水平直线上).已知AB=80m,DE=10m,求障碍物B,C两点间的距离是( )
(结果保留根号)
 如图,大楼AB的右侧有一障碍物,在障碍物的旁边有一幢小楼DE,在小楼的顶端D处测得障碍物边缘点C的俯角为30°,测得大楼顶端A的仰角为45°(点B,C,E在同一水平直线上).已知AB=80m,DE=10m,求障碍物B,C两点间的距离是( )
如图,大楼AB的右侧有一障碍物,在障碍物的旁边有一幢小楼DE,在小楼的顶端D处测得障碍物边缘点C的俯角为30°,测得大楼顶端A的仰角为45°(点B,C,E在同一水平直线上).已知AB=80m,DE=10m,求障碍物B,C两点间的距离是( )(结果保留根号)
| A. | 50 | B. | 70-10$\sqrt{3}$ | C. | 70+10$\sqrt{3}$ | D. | 70-$\frac{10\sqrt{3}}{3}$ |