题目内容
1.关于x的一元二次方程(m2-4)x2+(2m+3)x+1=0.①若此方程有解,试求m的取值范围;
②是否存在实数m,使此方程的两根的倒数和为7?若存在,请求出m的值;若不存在,试说明理由.
分析 ①根据一元二次方程的定义和判别式的意义得到m2-4≠0且△=(2m+3)2-4(m2-4)≥0,然后求出两不等式的公共部分即可;
②设方程的两根为x1、x2,根据根与系数的关系可得出x1+x2=-$\frac{2m+3}{{m}^{2}-4}$、x1•x2=$\frac{1}{{m}^{2}-4}$,$\frac{1}{{x}_{1}}$+$\frac{1}{{x}_{2}}$变形为$\frac{{x}_{1}+{x}_{2}}{{x}_{1}{x}_{2}}$,代入数据即可得出关于m的分式方程,解方程经检验后即可得出结论.
解答 解:①根据题意得m2-4≠0且△=(2m+3)2-4(m2-4)≥0,
解得m≥-$\frac{25}{12}$且m≠±2;
②设方程的两根为x1、x2,
根据根与系数的关系可得出
x1+x2=-$\frac{2m+3}{{m}^{2}-4}$、x1•x2=$\frac{1}{{m}^{2}-4}$,$\frac{1}{{x}_{1}}$+$\frac{1}{{x}_{2}}$=$\frac{{x}_{1}+{x}_{2}}{{x}_{1}{x}_{2}}$=-2m-3=7,
∴m=-5.
点评 本题考查了一元二次方程ax2+bx+c=0(a≠0)的根的判别式△=b2-4ac:当△>0,方程有两个不相等的实数根;当△=0,方程有两个相等的实数根;当△<0,方程没有实数根.也考查了一元二次方程的定义.

练习册系列答案
 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案
相关题目
10.在-3,-2、0、2这四个数中,最大的数是( )
| A. | -3 | B. | -2 | C. | 0 | D. | 2 |
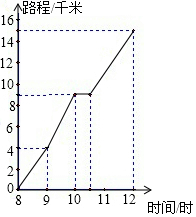 图为一位旅行者在早晨8时从城市出发到郊外所走的路程与时间的变化图.根据图象回答问题:
图为一位旅行者在早晨8时从城市出发到郊外所走的路程与时间的变化图.根据图象回答问题: