题目内容
如图，Rt△ABC中，AB=9，BC=6，∠B=90°，将△ABC折叠，使A点与BC的中点D重合，折痕为MN，则线段BN的长为考点：翻折变换（折叠问题）
专题：
分析：设BN=x，则由折叠的性质可得DN=AN=9-x，根据中点的定义可得BD=3，在Rt△ABC中，根据勾股定理可得关于x的方程，解方程即可求解．
解答：解：设BN=x，由折叠的性质可得DN=AN=9-x，
∵D是BC的中点，
∴BD=3，
在Rt△ABC中，x2+32=（9-x）2，
解得x=4．
故线段BN的长为4．
故答案为：4．
∵D是BC的中点，
∴BD=3，
在Rt△ABC中，x2+32=（9-x）2，
解得x=4．
故线段BN的长为4．
故答案为：4．
点评：此题考查了翻折变换（折叠问题），折叠的性质，勾股定理，中点的定义以及方程思想，综合性较强．
练习册系列答案
教材全解字词句篇系列答案
相关题目
观察下列球的排列规律（其中●是实心球，
是空心球）：
从第一个球起到第2013个球止，共有实心球（ ）个．
是空心球）：从第一个球起到第2013个球止，共有实心球（ ）个．
| A、201 | B、202 |
| C、604 | D、603 |
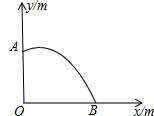为使自己在即将到来的体育达标测试推铅球项目中取得好成绩，初三某同学校长在体育课练习推铅球，某次投掷路线如图所示，铅球在点A处出手，在点B处落地，它的运行路线是一条抛物线，若在平面直角坐标系中，这条抛物线关系式为y=-
如图，△ABC中，AB=AC，BD⊥AC，垂足为D，sin∠DBC=
已知在纸面上有一数轴（如图），折叠纸面．