题目内容
已知4x2+y2-4x+6y+10=0，求2x-5y的平方根．
考点：配方法的应用,非负数的性质：偶次方,平方根
专题：
分析：通过观察、比较、分析，首先将所给方程的左边重新组合，运用完全平方公式转化为两个非负数和的形式，借助非负数的性质问题即可解决．
解答：解：∵4x2+y2-4x+6y+10=0，
∴（4x2-4x++1）+（y2+6y+9）=0
故（2x-1）2+（y+3）2=0；
∵（2x-1）2≥0，（y+3）2≥0，
∴2x-1=0，y+3=0
故x=
，y=-3；
∴2x-5y=2×
-5×（-3）=1+15=16，
2x-5y的平方根为±4．
∴（4x2-4x++1）+（y2+6y+9）=0
故（2x-1）2+（y+3）2=0；
∵（2x-1）2≥0，（y+3）2≥0，
∴2x-1=0，y+3=0
故x=
| 1 |
| 2 |
∴2x-5y=2×
| 1 |
| 2 |
2x-5y的平方根为±4．
点评：该命题借助平方根的定义，考查了学生的观察、分析、比较、探究能力；配方法及其应用能力．
练习册系列答案
相关题目
下列各选项正确的是（ ）
| A、0.10（精确到0.1） |
| B、0.05（精确到十分位） |
| C、5.5万（精确到千位） |
| D、1.205×107（精确到0.001） |
若y=mxm2+m+1是一次函数，则m的值为（ ）
| A、0 | B、-1 | C、0或-1 | D、±1 |
一个点从数轴原点开始，先向右移动3个单位长度，再向右移动2个单位长度，如图所示，由图可以看出，到达的终点是表示5的点．画图表示一个点在数轴上按如下方式移动达到的终点，并说明它表示的是什么数的点，从原点开始向右移动-4个单位长度，再向左移动-3个长度单位．
如图，Rt△ABC中，AB=9，BC=6，∠B=90°，将△ABC折叠，使A点与BC的中点D重合，折痕为MN，则线段BN的长为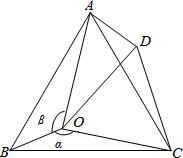
如图所示，点O是等边△ABC内一点，∠BOC=α，∠AOB=β（α、β均不是锐角），将△BOC绕点C按顺时针方向旋转60°得△ADC，连接OD．