题目内容
 如图,△ABC中,AB=AC,BD⊥AC,垂足为D,sin∠DBC=
如图,△ABC中,AB=AC,BD⊥AC,垂足为D,sin∠DBC=| 2 |
| 7 |
(1)求
| BC |
| AC |
(2)如果△ABC的周长18,求△ABC的面积.
考点:解直角三角形,等腰三角形的性质
专题:
分析:(1)如图,过点A作AE⊥BC于点E,则点E是BC的中点.通过解直角△BCD求得
=
,故
=
,则即
=
;
(2)利用三角形的周长公式求得三角形的三边长度,然后通过勾股定理求得AE的长度,则利用三角形的面积公式进行解答.
| EC |
| AC |
| 2 |
| 7 |
| ||
| AC |
| 2 |
| 7 |
| BC |
| AC |
| 4 |
| 7 |
(2)利用三角形的周长公式求得三角形的三边长度,然后通过勾股定理求得AE的长度,则利用三角形的面积公式进行解答.
解答: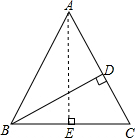 解:(1)如图,过点A作AE⊥BC于点E.
解:(1)如图,过点A作AE⊥BC于点E.
∵AB=AC,
∴点E是BC的中点.
又∵BD⊥AC,垂足为D,sin∠DBC=
.
∴cos∠ECA=sin∠DBC=
,即
=
,
∴
=
,则
=
;
(2)由(1)知,
=
.
故设AC=7a,BC=4a.
依题意得 14a+4a=18,
解得 a=1.
则AC=7,BC=4.
∴在直角△AEC中,由勾股定理得:AE=
=
=3
,
则△ABC的面积=
BC•AE=
×4×3
=6
.
 解:(1)如图,过点A作AE⊥BC于点E.
解:(1)如图,过点A作AE⊥BC于点E.∵AB=AC,
∴点E是BC的中点.
又∵BD⊥AC,垂足为D,sin∠DBC=
| 2 |
| 7 |
∴cos∠ECA=sin∠DBC=
| 2 |
| 7 |
| EC |
| AC |
| 2 |
| 7 |
∴
| ||
| AC |
| 2 |
| 7 |
| BC |
| AC |
| 4 |
| 7 |
(2)由(1)知,
| BC |
| AC |
| 4 |
| 7 |
故设AC=7a,BC=4a.
依题意得 14a+4a=18,
解得 a=1.
则AC=7,BC=4.
∴在直角△AEC中,由勾股定理得:AE=
| AC2-EC2 |
| 72-22 |
| 5 |
则△ABC的面积=
| 1 |
| 2 |
| 1 |
| 2 |
| 5 |
| 5 |
点评:本题考查了解直角三角形和等腰三角形的性质.此题利用勾股定理求得AE的长度.

练习册系列答案
相关题目
为了加快4G网络建设,某市电信运营企业将根据各自发展规划,今年预计完成3G投资3.8亿元左右,将3.8亿元用科学记数法表示时,下列记法正确的是( )
| A、3.8×103元 |
| B、3.8×106元 |
| C、3.8×107元 |
| D、3.8×108元 |
 如图,Rt△ABC中,AB=9,BC=6,∠B=90°,将△ABC折叠,使A点与BC的中点D重合,折痕为MN,则线段BN的长为
如图,Rt△ABC中,AB=9,BC=6,∠B=90°,将△ABC折叠,使A点与BC的中点D重合,折痕为MN,则线段BN的长为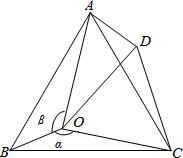 如图所示,点O是等边△ABC内一点,∠BOC=α,∠AOB=β(α、β均不是锐角),将△BOC绕点C按顺时针方向旋转60°得△ADC,连接OD.
如图所示,点O是等边△ABC内一点,∠BOC=α,∠AOB=β(α、β均不是锐角),将△BOC绕点C按顺时针方向旋转60°得△ADC,连接OD.