题目内容
9. 如图所示,在Rt△ABC中,∠C=90°,∠B=60°.
如图所示,在Rt△ABC中,∠C=90°,∠B=60°.(1)尺规作图:作线段AB的垂直平分线m(保留作图痕迹,不写作法);
(2)在已作的图形中,若直线m分别交AB、AC及BC的延长线于点D、E、F.连结AF,若AF=2,求△ABC的周长.
分析 (1)作线段AB的垂直平分线m即可;
(2)先根据线段垂直平分线的性质得出AF=BF,再由∠B=60°得出△ABF为等边三角形,由等边三角形三线合一的性质得出BC的长.再由勾股定理求出AC的长,进而可得出结论.
解答 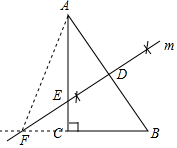 解:(1)如图,直线M即为所求;
解:(1)如图,直线M即为所求;
(2)∵直线DF垂直平分线段AB,
∴AF=BF.
∵AF=2,
∴BF=2.
∵∠B=60°.
∴△ABF为等边三角形,AB=2,
∴由等边三角形三线合一,AC垂直平分线段BF,BC=$\frac{1}{2}$BF=$\frac{1}{2}$×2=1.
∴Rt△ABC中,AC=$\sqrt{A{B}^{2}-B{C}^{2}}$=$\sqrt{4-1}$=$\sqrt{3}$.
∴△ABC周长=AB+BC+AC=2+1+$\sqrt{3}$=3+$\sqrt{3}$.
点评 本题考查的是作图-基本作图、线段垂直平分线的性质、勾股定理及等边三角形的性质等知识,熟知线段垂直平分线的作法是解答此题的关键.

练习册系列答案
 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案
相关题目
4. 点A、B、C、D都在如图所示的由正方形组成的网格图中,且线段CD与线段AB成位似图形,则位似中心为( )
点A、B、C、D都在如图所示的由正方形组成的网格图中,且线段CD与线段AB成位似图形,则位似中心为( )
 点A、B、C、D都在如图所示的由正方形组成的网格图中,且线段CD与线段AB成位似图形,则位似中心为( )
点A、B、C、D都在如图所示的由正方形组成的网格图中,且线段CD与线段AB成位似图形,则位似中心为( )| A. | 点E | B. | 点F | C. | 点H | D. | 点G |
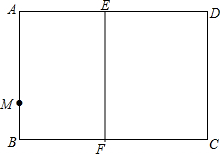 如图,在矩形纸片ABCD中,AB=4,BC=5,点E在AD边上,EF⊥BC,垂足为F,点M在AB边上,BM=1,沿过点M的直线折叠该纸片,使点A落在线段EF上的点A'处,折痕为 MN,点N在AD边上.
如图,在矩形纸片ABCD中,AB=4,BC=5,点E在AD边上,EF⊥BC,垂足为F,点M在AB边上,BM=1,沿过点M的直线折叠该纸片,使点A落在线段EF上的点A'处,折痕为 MN,点N在AD边上. 如图,在△ABC中,DE∥BC中,AD=1,BD=2,DE=2,求BC的长.
如图,在△ABC中,DE∥BC中,AD=1,BD=2,DE=2,求BC的长.