题目内容
课外兴趣小组活动时,老师提出了如下问题:
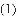
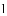
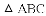
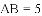
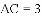
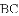
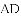
小明在组内经过合作交流,得到了如下的解决方法:延长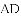
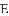
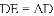
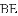
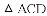
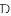
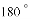 得到
得到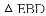
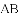
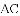
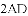
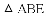
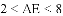
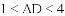
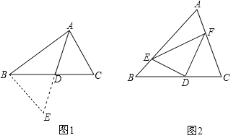
[感悟]解题时,条件中若出现“中点”“中线”字样,可以考虑构造以中点为对称中心的中心对称图形,把分散的已知条件和所求证的结论集中到同一个三角形中.
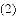
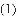
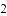
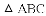
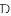
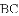
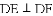
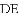
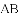
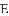
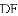
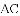
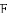
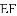
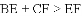
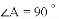 ,探索线段
,探索线段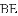
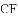
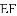
练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目


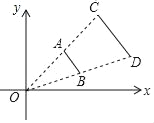
 B. 1,
B. 1,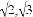
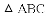
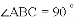 ,
,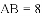
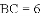
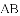
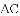
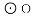
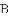
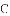
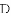
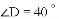 ,则
,则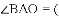

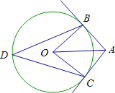
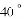 B.
B. 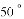 C.
C. 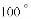 D.
D. 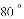
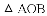
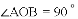 ,
,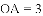
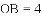
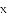
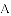



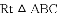
 ,
, ,
,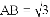 ,将
,将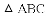
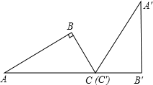
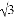 C.
C. 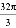 D.
D.