题目内容
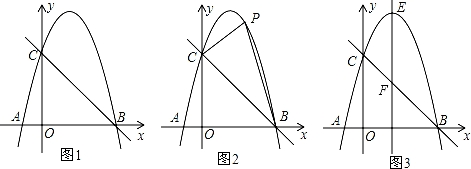
如图,所示,已知抛物线经过点A(-1,0),B(3,0),C(0,3)三点。
(1)求抛物线的解析式;
(2)点M是线段BC上的点(不与B,C重合),过M做MN∥y轴交抛物线于N,若点M的横坐标为m,请用m的代数式表示MN的长。
(3)在(2)的条件下,连接NB,NC,是否存在m,使△BNC的面积最大?若存在,求m的值;若不存在,说明理由。
 |
解:(1)设y=ax²+bx+c
则 0=a-b+c
0=9a+3b+c
3=c
∴ a=﹣1
b=2
C=﹣3
∴y=﹣x²+2x-3……3分
(2)设直线BL的解析式为
y= k x+b
则 3k+b=0 k=﹣1
b=3 b=3
∴y=﹣x+3
∴ M(m,﹣m+3)
N(m,﹣m²+2m+3)
∴MN=﹣m²+2m+3-(-m+3)
=﹣m²+3m
(0<m<3)…………6分
(3)∵S△BCN=S△CMN+S△BMN=

= (0<m<3)
(0<m<3)
∴ 当 时,S最大=
时,S最大= ……9分
……9分

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目


 ,使△
,使△