题目内容
1.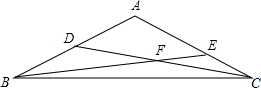 在△ABC中,D为AB的中点,∠CDA=45°,E在AC上,连接BE交CD于F,满足EF=EC,△CBF的面积为8,则CF=4$\sqrt{2}$.
在△ABC中,D为AB的中点,∠CDA=45°,E在AC上,连接BE交CD于F,满足EF=EC,△CBF的面积为8,则CF=4$\sqrt{2}$.
分析 延长CD到G,使DG=CD,过B作BH⊥DG于H,根据全等三角形的性质得到∠G=∠ACD,S△ACD=S△BDG=S△CBD,根据等腰三角形的性质得到GH=FH,得到S△BHG=S△BFH,设△BDH的面积=x,△BFD的面积=y,
则△BHG的面积=x+y,列方程得到S△BDH=4,根据等腰直角三角形的性质得到BH=2$\sqrt{2}$,于是得到结论.
解答 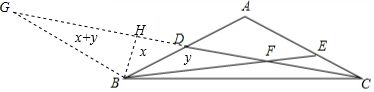 解:延长CD到G,使DG=CD,
解:延长CD到G,使DG=CD,
过B作BH⊥DG于H,
∵D为AB的中点,
∴AD=DB,
在△ACD与△BGD中,$\left\{\begin{array}{l}{AD=BD}\\{∠ADC=∠BDG}\\{CD=DG}\end{array}\right.$,
∴△ACD≌△BGD,
∴∠G=∠ACD,S△ACD=S△BDG=S△CBD,
∵EF=EC,
∴∠CFE=∠ECF,
∵∠EFB=∠EFC,
∴∠G=∠BFD,
∴BG=BF,
∴GH=FH,
∴S△BHG=S△BFH,设△BDH的面积=x,△BFD的面积=y,
则△BHG的面积=x+y,
∴x+x+y=y+8,
∴x=4,
∴S△BDH=4,
∵∠BDH=∠ADC=45°,
∴BH=DH,
∴BH=2$\sqrt{2}$,
∵△CBF的面积为8,
∴CF=4$\sqrt{2}$.
故答案为:4$\sqrt{2}$.
点评 本题考查了三角形的面积,全等三角形的判定和性质,正确的作出辅助线是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
11. 如图,△ABC和△DCE都是直角三角形,其中一个三角形是由另一个三角形旋转得到的,下列叙述中错误的是( )
如图,△ABC和△DCE都是直角三角形,其中一个三角形是由另一个三角形旋转得到的,下列叙述中错误的是( )
 如图,△ABC和△DCE都是直角三角形,其中一个三角形是由另一个三角形旋转得到的,下列叙述中错误的是( )
如图,△ABC和△DCE都是直角三角形,其中一个三角形是由另一个三角形旋转得到的,下列叙述中错误的是( )| A. | 旋转中心是点C | |
| B. | 顺时针旋转角是90° | |
| C. | 旋转中心是点B,旋转角是∠ABC | |
| D. | 既可以是逆时针旋转又可以是顺时针旋转 |
 已知如图,在三角形ABC中,AC⊥AB,DG⊥BC,EF⊥AB,∠1=∠2,试判断CD与AB的位置关系?并说明理由.
已知如图,在三角形ABC中,AC⊥AB,DG⊥BC,EF⊥AB,∠1=∠2,试判断CD与AB的位置关系?并说明理由.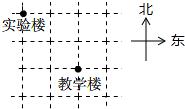 某学校的平面示意图如图所示,请用两种不同的方法表示出实验楼相对于教学楼的位置.图中小方格边长代表实地距离50(单位:m),对角线长代表实地距离70.7(单位:m).
某学校的平面示意图如图所示,请用两种不同的方法表示出实验楼相对于教学楼的位置.图中小方格边长代表实地距离50(单位:m),对角线长代表实地距离70.7(单位:m). 如图,已知直线AB,CD被直线EF所截,若∠A=75°,∠C=105°,∠AEF=60°,则∠EFD的度数为60°.
如图,已知直线AB,CD被直线EF所截,若∠A=75°,∠C=105°,∠AEF=60°,则∠EFD的度数为60°.