Question

17．已知抛物线的顶点坐标为（-1，2），且过点（1，-2）
（1）求抛物线的函数表达式；
（2）求抛物线与坐标轴的交点坐标；
（3）画出此函数图象的草图，并根据图象回答：x为何值时，y＞0？

Answer 1

分析 （1）由于已知抛物线的顶点坐标，则可设顶点式y=a（x+1）²+2，然后把（1，-2）代入求出a即可．
（2）分别令x=0和令y=0求得抛物线与坐标轴的交点坐标；
（3）根据求得的交点坐标和对称轴即可作出草图并确定什么时候y＞0．

解答 解：（1）设抛物线解析式为y=a（x+1）²+2，
把（1，-2）代入得4a+2=-2，解得a=-1，
所以抛物线解析式为y=-（x+1）²+2．
（2）当x=0时，y=1，
∴它与y轴的交点坐标为（0，1）
当y=0时，x²-2x-3=0
解得：x=-1+$\sqrt{2}$或x=-1-$\sqrt{2}$
∴它与x轴的交点坐标为（-1+$\sqrt{2}$，0）和（-1-$\sqrt{2}$，0）
（3）画出函数图象如图：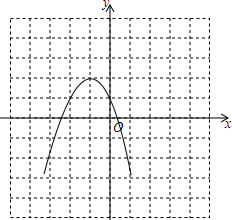

当-1-$\sqrt{2}$x＜-1+$\sqrt{2}$时，y＞0．

点评 本题考查了待定系数法求二次函数的解析式，在利用待定系数法求二次函数关系式时，要根据题目给定的条件，选择恰当的方法设出关系式，从而代入数值求解．一般地，当已知抛物线上三点时，常选择一般式，用待定系数法列三元一次方程组来求解；当已知抛物线的顶点或对称轴时，常设其解析式为顶点式来求解；当已知抛物线与x轴有两个交点时，可选择设其解析式为交点式来求解．还考查了二次函数的图象以及二次函数和不等式的关系．