题目内容
7.探究:有一长6cm,宽4cm的矩形纸板,现要求以其一组对边中点所在直线为轴,旋转180°,得到一个圆柱,现可按照两种方案进行操作:方案一:以较长的一组对边中点所在直线为轴旋转,如图①;
方案二:以较短的一组对边中点所在直线为轴旋转,如图②.
(1)请通过计算说明哪种方法构造的圆柱体积大;
(2)如果该矩形的长宽分别是5cm和3cm呢?请通过计算说明哪种方法构造的圆柱体积大;
(3)通过以上探究,你发现对于同一个矩形(不包括正方形),以其一组对边中点所在直线为轴旋转得到一个圆柱,怎样操作所得到的圆柱体积大(不必说明原因)?

分析 (1)根据矩形旋转是圆柱,可得几何体,根据圆柱的体积公式,可得答案;
(2)根据矩形旋转是圆柱,可得几何体,根据圆柱的体积公式,可得答案;
(3)根据矩形旋转所的几何体的大小比较,可得答案.
解答 解:(1)方案一:π×32×4=36π(cm3),
方案二:π×22×6=24π(cm3),
∵36π>24π,
∴方案一构造的圆柱的体积大;
(2)方案一:π×($\frac{5}{2}$)2×3=$\frac{75}{4}$π(cm3),
方案二:π×($\frac{3}{2}$)2×5=$\frac{45}{4}$π(cm3),
∵$\frac{75}{4}$π>$\frac{45}{4}$π,
∴方案一构造的圆柱的体积大;
(3)由(1)、(2),得
以较长一组对边中点所在直线为轴旋转得到的圆柱的体积大.
点评 本题考查了点线面体,利用矩形旋转得圆柱是解题关键.

练习册系列答案
相关题目
15.下列方程中是一元一次方程的是( )
| A. | x-3=2x | B. | x2=1 | C. | 2x+y=1 | D. | $\frac{2}{x}$-1=0 |
19. 如图所示的一块地,∠ADC=90°,AD=12m,CD=9m,AB=39m,BC=36m,求这块地的面积S为( )cm2.
如图所示的一块地,∠ADC=90°,AD=12m,CD=9m,AB=39m,BC=36m,求这块地的面积S为( )cm2.
 如图所示的一块地,∠ADC=90°,AD=12m,CD=9m,AB=39m,BC=36m,求这块地的面积S为( )cm2.
如图所示的一块地,∠ADC=90°,AD=12m,CD=9m,AB=39m,BC=36m,求这块地的面积S为( )cm2.| A. | 54 | B. | 108 | C. | 216 | D. | 270 |
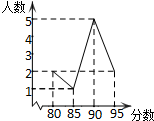 某班10名学生成绩统计如图,则这10名学生成绩中位数是90分,众数是90分.
某班10名学生成绩统计如图,则这10名学生成绩中位数是90分,众数是90分. 要从甲、乙两名同学中选出一名,代表班级参加射击比赛,如图是两人最近10次射击训练成绩的折线统计图.(两同学的射击成绩都取整数环)
要从甲、乙两名同学中选出一名,代表班级参加射击比赛,如图是两人最近10次射击训练成绩的折线统计图.(两同学的射击成绩都取整数环) 如图,两根高度分别是2米和3米的直杆AB、CD竖直在水平地面MN上,相距12米,现要从A点拉一根绳索,接地后再拉到C点处,为了节省绳索材料,请问:
如图,两根高度分别是2米和3米的直杆AB、CD竖直在水平地面MN上,相距12米,现要从A点拉一根绳索,接地后再拉到C点处,为了节省绳索材料,请问: 如图,把两个大小相同的含30°的角的三角尺如图放置,若AD=4$\sqrt{6}$,试求围成的△ADC的面积.
如图,把两个大小相同的含30°的角的三角尺如图放置,若AD=4$\sqrt{6}$,试求围成的△ADC的面积.