题目内容
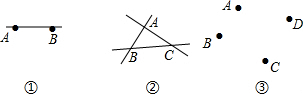
6．如图①，点A和点B可确定1条直线，观察图②，不在同一直线上的三点A、B、C最多能确定3条直线．（1）动手画一画图③中经过A、B、C、D四点中任意两点的所有直线，最多能作6条直线；
（2）在同一平面内的五个点，任三点不在同一直线上，过其中两点作直线，最多能作10条，共n个点（n≥2）时最多能作$\frac{n（n-1）}{2}$条直线．
分析 根据两点确定一条直线可得出①的答案；动手画出图形可得出②的答案，注意根据特殊总结出一般规律．
解答 解：（1）经过A、B、C、D四点最多能确定6条直线；
（2）直在同一平面内任三点不在同一直线的五个点最多能确定10条线、
根据1个点、两个点、三个点、四个点、五个点的情况可总结出n个点（n≥2）时最多能确定：$\frac{n（n-1）}{2}$条直线．
故答案为：6，10，$\frac{n（n-1）}{2}$．
点评 本题考查了点确定直线的知识，有一定难度，注意动手操作及总结规律能力的培养．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
如图，把边长为2cm的正方形剪成四个全等的直角三角形，请用这四个直角三角形拼成符合下列要求的图形（全部用上，互不重叠且不留空隙），把你的拼法画出来．（设每个方格边长为1cm）
已知a，b，c为有理数，且它们在数轴上的位置如图所示．