Question

7．如图，已知E为圆内两弦AB和CD的交点，直线EF∥CB，交AD的延长线于F，FG切圆于G．求证：EF=FG．

Answer 1

分析 根据相似三角形的判定定理证明△FED∽△FAE，根据相似三角形的性质定理得到EF²=FD•FA，根据切割线定理得到GF²=FD•FA，等量代换证明结论．

解答 解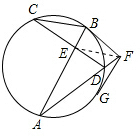：连接EF，
∵EF∥CB，
∴∠BCD=∠FED，又∠BCD=∠BAD，
∴∠BCD=∠FED，又∠EFD=∠EFD，
∴△FED∽△FAE，
∴$\frac{EF}{FA}$=$\frac{DF}{EF}$，
∴EF²=FD•FA，
∵FG切圆于G，
∴GF²=FD•FA，
∴EF=FG．

点评 本题考查的是切线的性质、相似三角形的判定和性质，掌握切割线定理、相似三角形的判定定理和性质定理是解题的关键．