题目内容
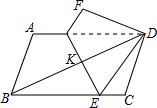 如图,已知四边形ABCD中,AB∥CD,AB=
如图,已知四边形ABCD中,AB∥CD,AB=| 6 |
| 3 |
| 3 |
考点:翻折变换(折叠问题)
专题:
分析:如图,作辅助线,根据勾股定理求出CH、DH的长;再根据勾股定理求出BE的长;证明四边形BEDG为菱形,根据菱形的性质,结合面积公式即可解决问题.
解答:解:如图,连接BG,过点D作DH⊥BC,交BC的延长线于点H.
设CH=λ,DH=μ;
∵四边形ABCD是平行四边形,
∴DC=AB=
,由勾股定理得:
DH2+CH2=DC2,BH2+DH2=BD2,
即λ2+μ2=6,(2
+λ)2+μ2=(3+
)2,
解得:λ=
,μ=
,
设BE=γ,则EH=2
-γ+λ=
-γ;
由题意得:DE=BE=γ,根据勾股定理:
γ2=(
-γ)2+(
)2,
解得:γ=
+1;
由题意得:BK=DK,而平行四边形ABCD为中心对称图形,
∴GK=EK,而GE⊥BD,
∴四边形BEDG为菱形,
S菱形BEDG=
BD•GE=
BE•DH,
即
×(3+
)•GE=
(
+1)•
,
∴GE=
.
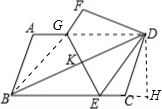
设CH=λ,DH=μ;
∵四边形ABCD是平行四边形,
∴DC=AB=
| 6 |
DH2+CH2=DC2,BH2+DH2=BD2,
即λ2+μ2=6,(2
| 3 |
| 3 |
解得:λ=
3-
| ||
| 2 |
3+
| ||
| 2 |
设BE=γ,则EH=2
| 3 |
3
| ||
| 2 |
由题意得:DE=BE=γ,根据勾股定理:
γ2=(
3
| ||
| 2 |
3+
| ||
| 2 |
解得:γ=
| 3 |
由题意得:BK=DK,而平行四边形ABCD为中心对称图形,
∴GK=EK,而GE⊥BD,
∴四边形BEDG为菱形,
S菱形BEDG=
| 1 |
| 2 |
| 1 |
| 2 |
即
| 1 |
| 2 |
| 3 |
| 1 |
| 2 |
| 3 |
3+
| ||
| 2 |
∴GE=
| ||
| 2 |

点评:该题主要考查了翻折变换及其性质的应用问题;解题的关键是根据翻折变换的性质找出图形中隐含的等量关系;灵活运用有关定理来分析、判断;对综合的分析问题解决问题的能力提出了较高的要求.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图,已知:AB⊥AE,AB=AC,AD⊥AE,AD=AE.求证:BE=CD.
如图,已知:AB⊥AE,AB=AC,AD⊥AE,AD=AE.求证:BE=CD. 如图,在△ABC中,AB=AC,D是AC上一点,过D作DE⊥BC于E,与BA的延长线交于F,求证:AD=AF.
如图,在△ABC中,AB=AC,D是AC上一点,过D作DE⊥BC于E,与BA的延长线交于F,求证:AD=AF.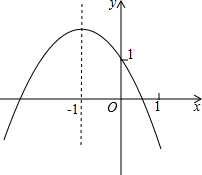 如图为二次函数y=ax2+bx+c(a≠0)的图象,下面四条信息:①4ac<b2<0;②4a+c<2b;③m(am+b)<a-b(m≠-1);④3a+c>0,其中正确信息的个数是( )
如图为二次函数y=ax2+bx+c(a≠0)的图象,下面四条信息:①4ac<b2<0;②4a+c<2b;③m(am+b)<a-b(m≠-1);④3a+c>0,其中正确信息的个数是( ) 如图,有一张直角三角形纸片,两直角边AC=5cm,BC=10cm,将△ABC折叠,点B与点A重合,折痕为DE,求CD的长.
如图,有一张直角三角形纸片,两直角边AC=5cm,BC=10cm,将△ABC折叠,点B与点A重合,折痕为DE,求CD的长.